Moltiplicatore di attivazione del meccanismo

(relazione C8A.4.1 della Circolare 617/2009)

Il moltiplicatore di attivazione del meccanismo 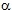₀ si ottiene applicando il principio dei lavori virtuali. Assegnata una rotazione virtuale al sistema è possibile calcolare gli spostamenti infinitesimi di tutti i punti di applicazione delle forze che partecipano al meccanismo. Generalizzando si ottiene la seguente espressione:

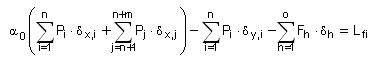
dove

-  “n” è il numero di tutte le forze peso applicate ai diversi blocchi della catena cinematica;

-  “m” è il numero di forze peso non direttamente gravanti sui blocchi, le cui masse, per effetto dell'azione sismica, generano forze orizzontali sugli elementi della catena cinematica (può essere il caso di solai che non poggiano direttamente sulla catena cinematica, ma sotto l’effetto del sisma generano una forza d’inerzia sulla catena stessa);

-  “o” è il numero di forze esterne, non associate a masse, applicate ai diversi blocchi;

-  “P_i” è la generica forza peso applicata;

-  “P_j” è la generica forza peso non direttamente gravante sui blocchi le cui masse, per effetto dell'azione sismica, generano forze orizzontali sugli elementi della catena cinematica;

-  d_x,i è lo spostamento virtuale orizzontale del punto di applicazione dell’i-esimo peso P_i, assumendo come verso positivo quello associato alla direzione secondo cui agisce l’azione sismica che attiva il meccanismo;

-  d_x,j è lo spostamento virtuale orizzontale del punto di applicazione dell’j-esimo peso P_j, assumendo come verso positivo quello associato alla direzione secondo cui agisce l’azione sismica che attiva il meccanismo;

-  d_y,i è lo spostamento virtuale verticale del punto di applicazione dell’i-esimo peso P_i, assunto positivo se verso l’alto;

-   F_h è la generica forza esterna (in valore assoluto), applicata ad un blocco;

-  d_h è lo spostamento virtuale del punto dove è applicata la h-esima forza esterna, nella direzione della stessa, di segno positivo se con verso discorde;

-  L_fi è il lavoro di eventuali forze interne.

La soluzione della precedente ci consente di individuare il moltiplicatore 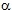₀.