Indicatore di rischio valutato con metodo semplificato
Poiché l’edificio è composto da due piani fuori terra, per valutare la vulnerabilità sismica dell’edificio occorre risolvere la relazione (1) quattro volte (una per ogni direzione principale ed una per ogni piano):
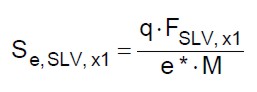 (13.a)
(13.a)
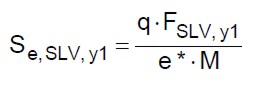 (13.b)
(13.b)
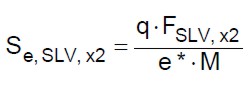 (13.c)
(13.c)
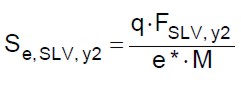 (13.d)
(13.d)
Il fattore di struttura q viene determinato in funzione delle prescrizioni di normativa tenendo conto che l’edificio è esistente, non regolare in altezza (dalla geometria dei due piani si intuisce subito che la struttura non presenta le caratteristiche di regolarità in altezza) ed a più piani. Sotto queste condizioni la normativa consiglia il seguente valore:
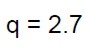 (14)
(14)
La frazione di massa partecipante può essere valutata attraverso la (12):
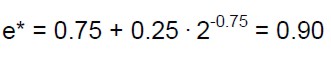 (15)
(15)
La massa M si ricava dalla (9). Per valutare il dato occorre valutare i carichi permanenti e variabili di tutta la struttura. Effettuando l’analisi dei carichi si ottengono i seguenti valori:
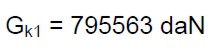 (16.a)
(16.a)
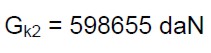 (16.b)
(16.b)
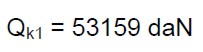 (16.c)
(16.c)
 (16.d)
(16.d)
Combinando le (16) secondo la (9) si ottiene:
 (17)
(17)
Per definire le (13) rimangono da valutare le resistenze a taglio per ogni direzione e per ogni piano (FSLV,x1, FSLV,y1, FSLV,x2 e FSLV,y2) date dalle (4). Per semplificare estremamente il problema (in questa fase dell’esempio), attribuiamo ai coefficienti che compaiono nelle (4) i valori più cautelativi:
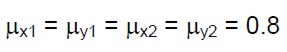 (18.a)
(18.a)
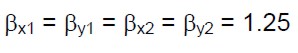 (18.b)
(18.b)
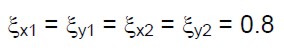 (18.c)
(18.c)
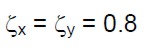 (18.d)
(18.d)
Il coefficiente  i si ricava dalle (6):
i si ricava dalle (6):
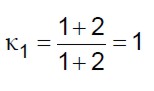 (19.a)
(19.a)
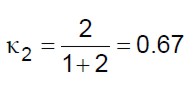 (19.b)
(19.b)
Nelle tabelle e figure successive si riportano le aree delle sezioni trasversali dei maschi murari in direzione x ed y e per il primo ed il secondo piano f.t. della costruzione.
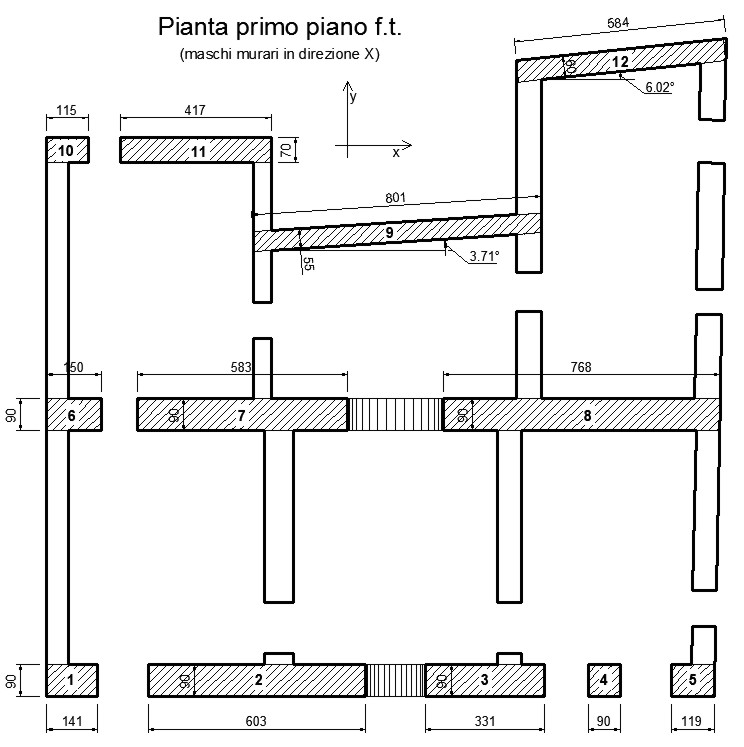
Figura 4.a – Maschi murari in direzione x del primo piano f.t.
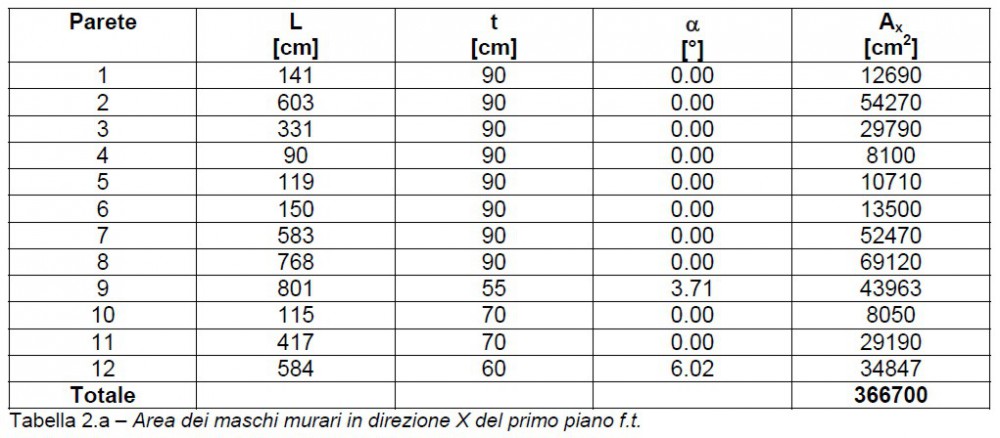
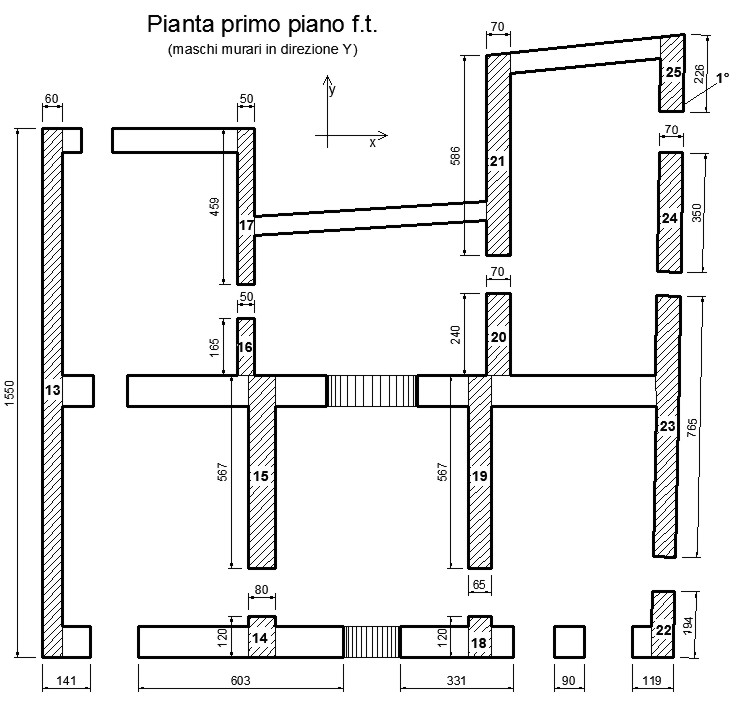
Figura 4.b – Maschi murari in direzione y del primo piano f.t.
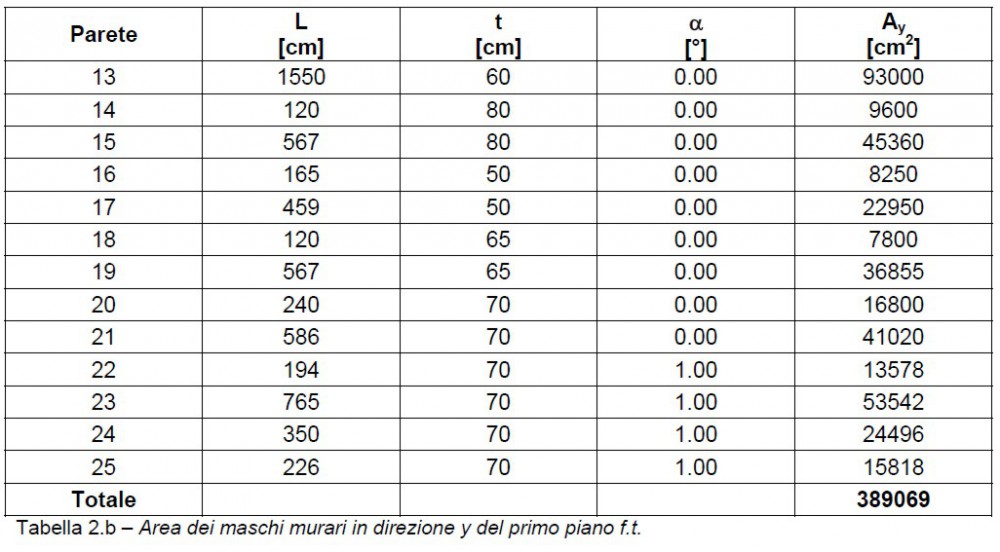
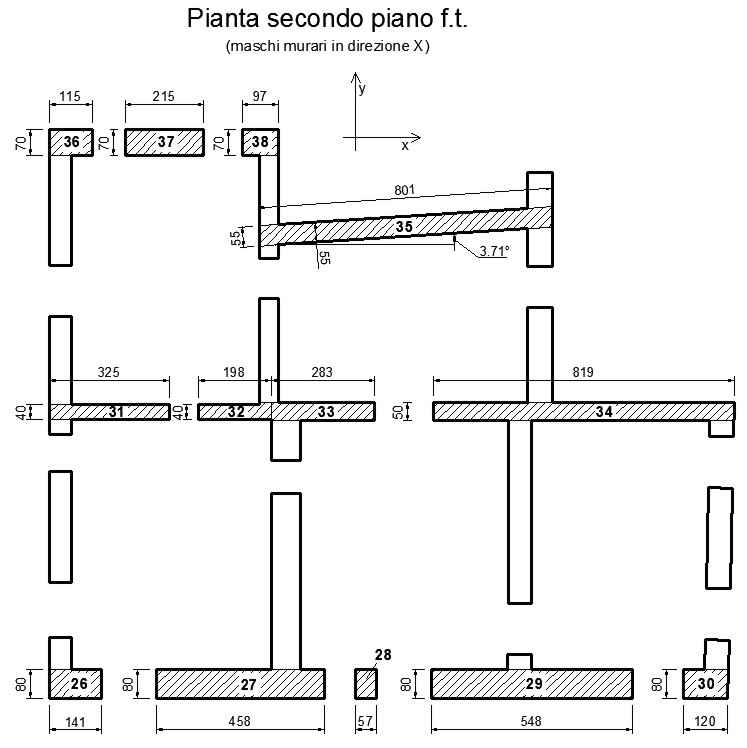
Figura 4.c – Maschi murari in direzione x del secondo piano f.t.
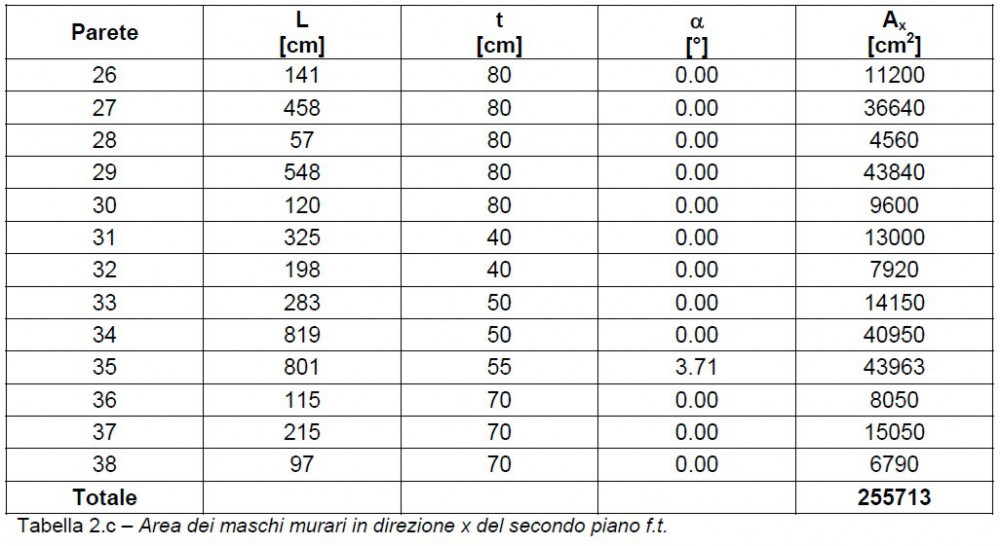
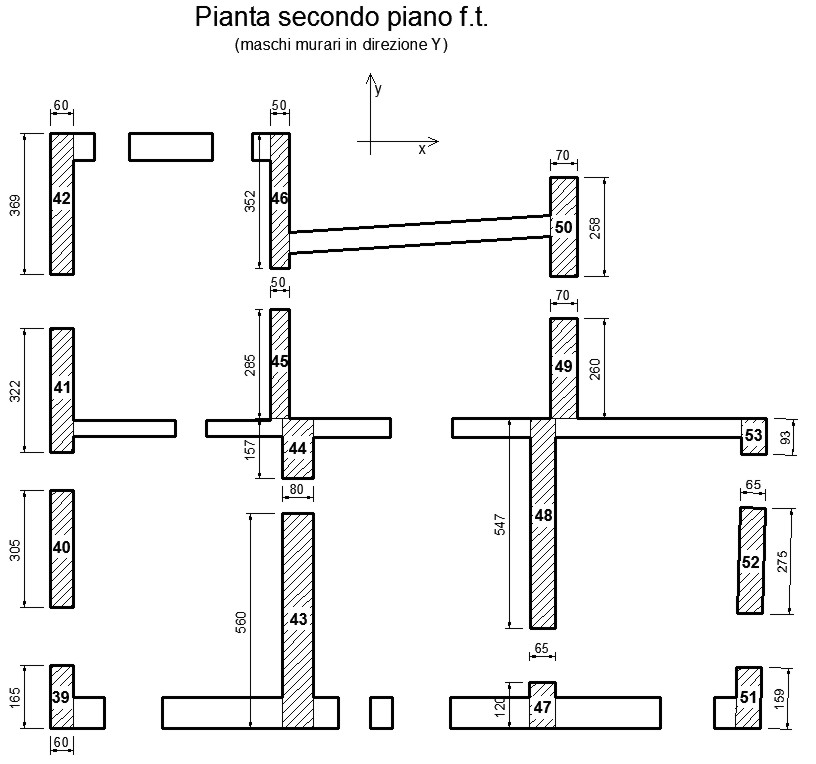
Figura 4.d – Maschi murari in direzione y del secondo piano f.t.
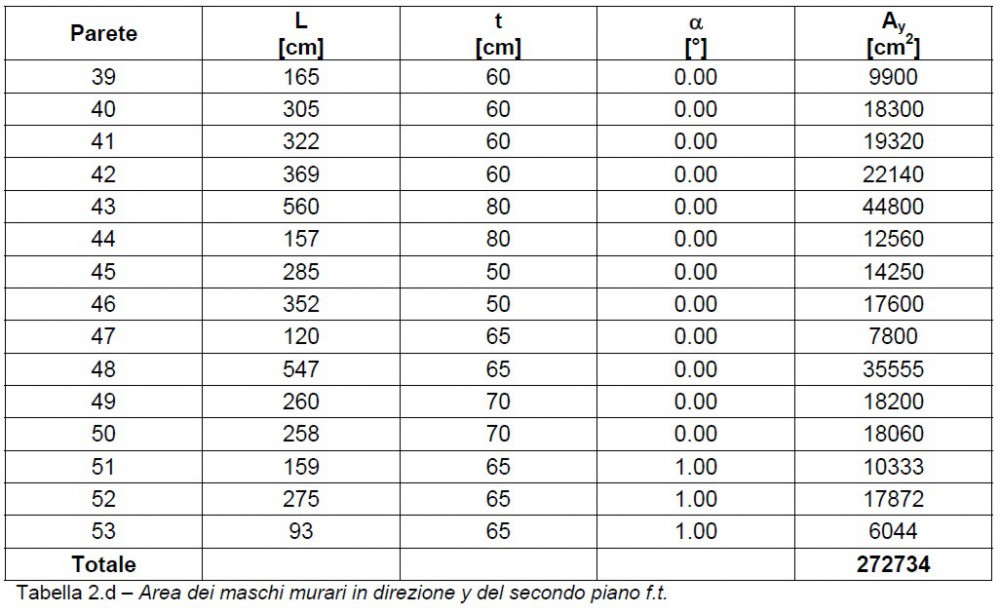
Nelle tabelle 2 si indica con L la lunghezza, con t lo spessore e con 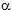 l’inclinazione rispetto alla direzione di ogni maschio murario.
l’inclinazione rispetto alla direzione di ogni maschio murario.
Per risolvere le (4) occorre ancora determinare la tensione  di data dalla (5). Per determinare la tensione verticale media
di data dalla (5). Per determinare la tensione verticale media  0i occorre definire l’area totale (At) di muratura resistente per ogni piano (l’area totale At non coincide con la somma delle aree Ax ed Ay ricavate nelle tabelle 3 in quanto c’è da tenere conto anche della sovrapposizione agli incroci tra i muri ortogonali: At < Ax + Ay). Nelle figure e tabelle successive si riporta l’area totale di muratura per ogni piano.
0i occorre definire l’area totale (At) di muratura resistente per ogni piano (l’area totale At non coincide con la somma delle aree Ax ed Ay ricavate nelle tabelle 3 in quanto c’è da tenere conto anche della sovrapposizione agli incroci tra i muri ortogonali: At < Ax + Ay). Nelle figure e tabelle successive si riporta l’area totale di muratura per ogni piano.
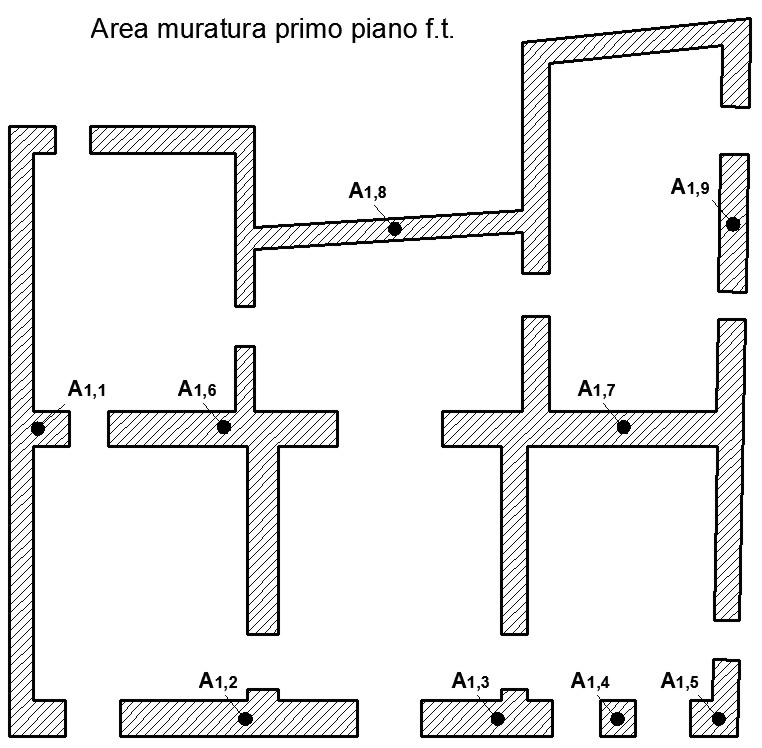
Figura 5.a – Area totale di muratura per il primo piano f.t.
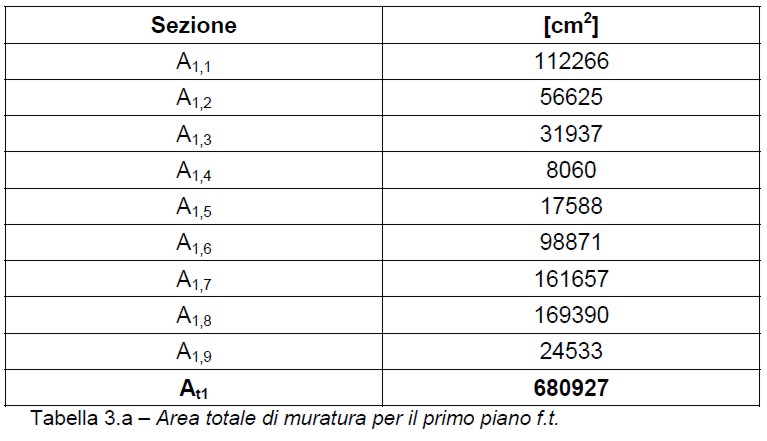
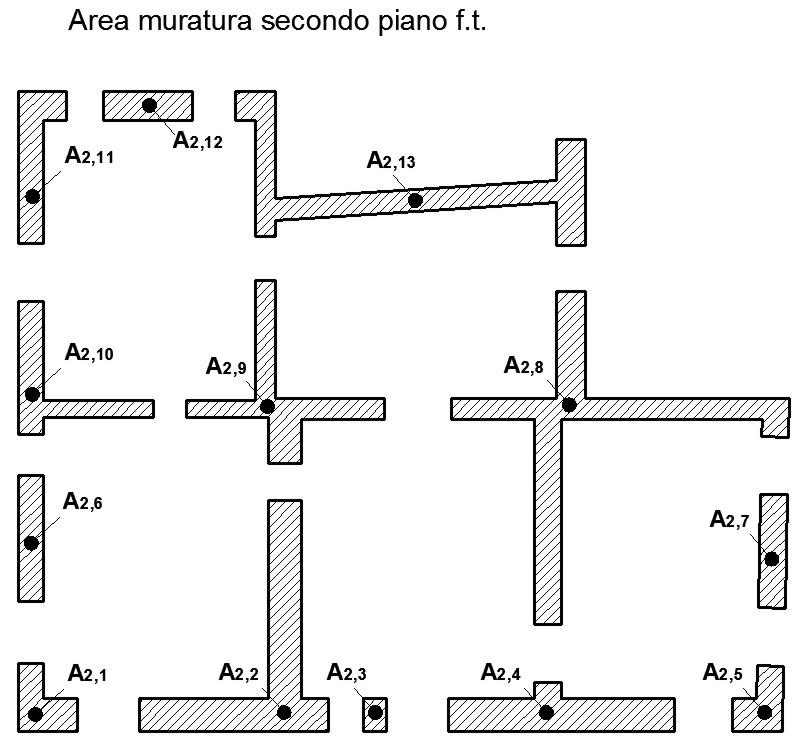
Figura 5.b – Area totale di muratura per il secondo piano f.t.
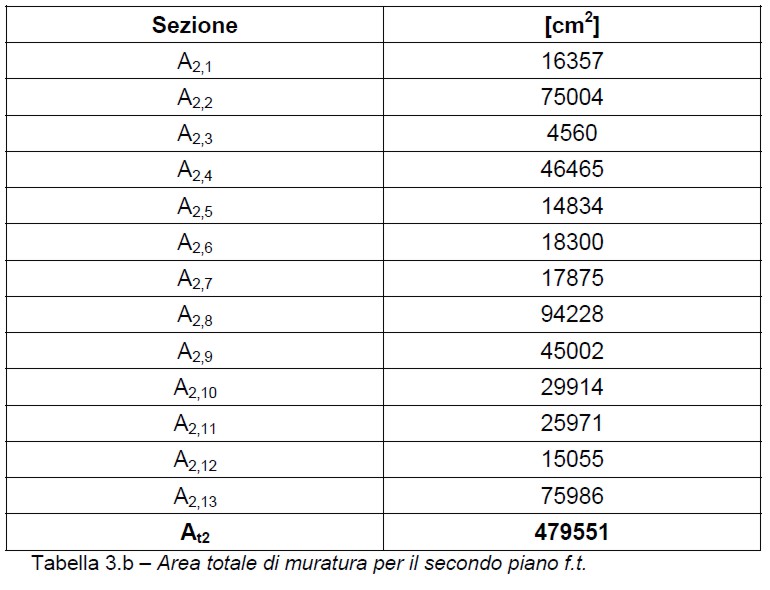
La tensione media  0i dell’i-esimo piano si ottiene dividendo lo sforzo normale medio Ni per l’area totale di muratura calcolata nelle tabelle 3. Le azioni Ni dell’i-esimo piano si possono ricavare direttamente dalle (16):
0i dell’i-esimo piano si ottiene dividendo lo sforzo normale medio Ni per l’area totale di muratura calcolata nelle tabelle 3. Le azioni Ni dell’i-esimo piano si possono ricavare direttamente dalle (16):
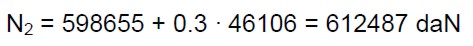 (20.a)
(20.a)
 (20.b)
(20.b)
Noti gli sforzi normali dati dalle (20) e le aree totali delle sezioni trasversali di muratura date dalle tabelle 3 è possibile valutare le tensioni medie  0i:
0i:
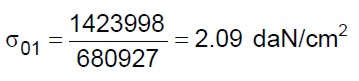 (21.a)
(21.a)
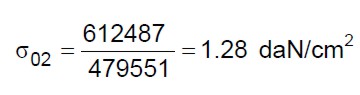 (21.b)
(21.b)
La muratura di cui è costituito l’edificio, può essere classificata di tipo “pietrame disordinata”. Poiché non sono state fatte prove distruttive sui materiali, il livello di conoscenza raggiunto è LC1. Per questo livello di conoscenza, i parametri meccanici si ricavano in funzione di quanto riportato nella Circolare 617/2009. Nella tabella 4 si riportano i dati relativi ai parametri meccanici minimi e massimi del materiale (definiti nella tabella C8A.2.1 della Circolare 617/2009).
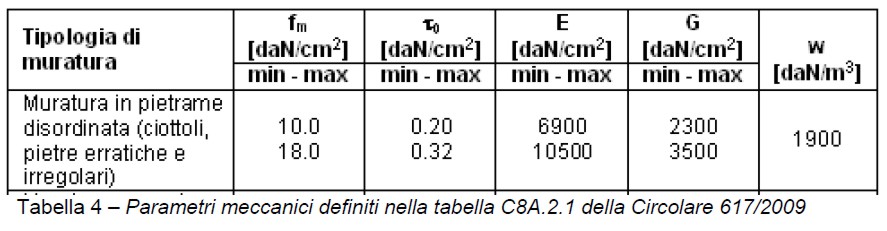
Visto che il livello di conoscenza è LC1, si deve assumere il valore minimo riportato in tabella per la tensione tangenziale. Tenendo conto che occorre dividere i valori delle resistenze per il fattore di confidenza che per LC1 vale 1.35 e per il coefficiente di sicurezza ( m) assunto pari a 2 si ottiene:
m) assunto pari a 2 si ottiene:
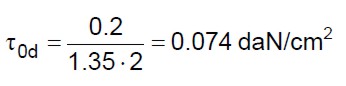 (22)
(22)
Dalla (5) e tenendo conto delle (21) e (22) è possibile valutare la tensione tangenziale di ogni piano:
 (23.a)
(23.a)
 (23.b)
(23.b)
A questo punto, attraverso le (4) è possibile valutare le resistenze a taglio relative a direzioni e piani:
 (24.a)
(24.a)
 (24.b)
(24.b)
 (24.c)
(24.c)
 (24.d)
(24.d)
Sostituendo i valori numerici nelle (13) si ottiene:
 (25.a)
(25.a)
 (25.b)
(25.b)
 (25.c)
(25.c)
 (25.d)
(25.d)
Il valore più basso è dato dalla (25.c) (secondo piano in direzione x). L’accelerazione che porta al raggiungimento dello stato limite si ottiene dalle (3). A tal proposito occorre valutare il periodo fondamentale della costruzione che può essere ricavato in via approssimativa dalla seguente:
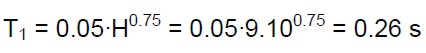 (26)
(26)
Per valutare la vulnerabilità occorre definire l’azione sismica di base i cui parametri vengono riassunti nella tabella 5.
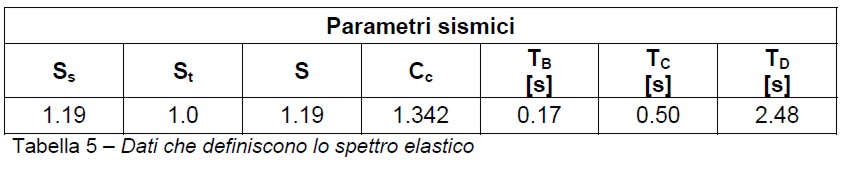
Poiché il periodo della struttura è compreso tra TB e TC ne consegue che per definire l’accelerazione di picco occorre considerare la prima delle (3). Note le quantità ag, F0 e T*C per i nove tempi di ritorno forniti dalla normativa (vedi tabella 6), è possibile valutare i corrispondenti valori di Se.
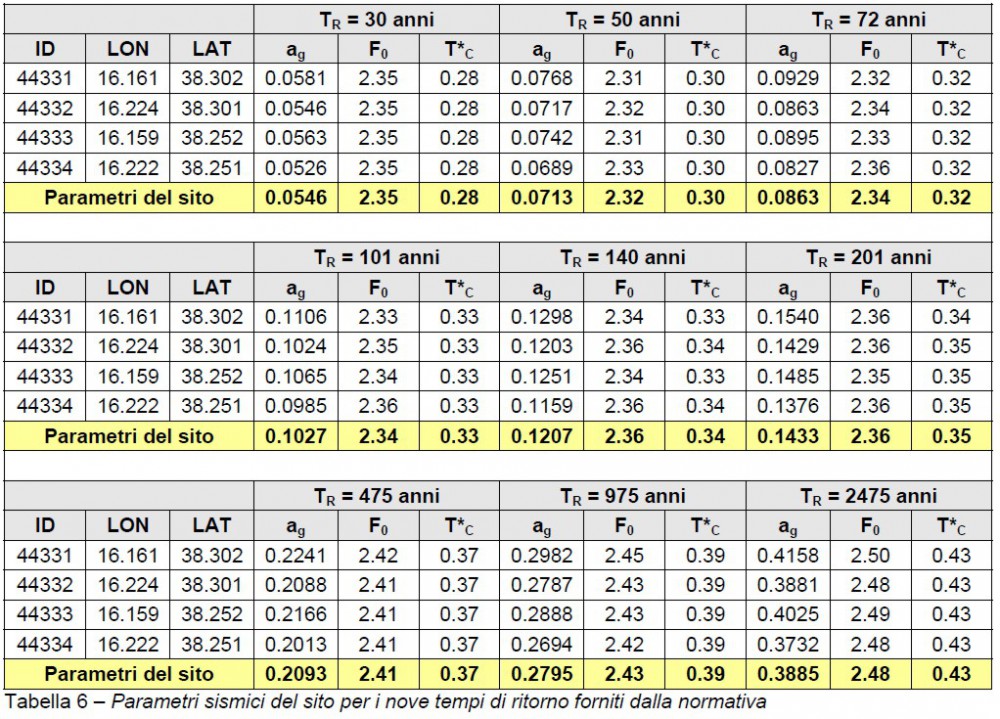

Tenendo conto della tabella 7 e delle (25) si deduce che il tempo di ritorno per lo stato limite SLV è inferiore a 30 anni. Dalle (3) e dalla (25.c) si ottiene:
 (27)
(27)
L’indicatore di rischio in termini di accelerazioni è dato dalla seguente (l’accelerazione di riferimento del sito per SLV si ottiene dalla tabella 7 in corrispondenza del periodo di ritorno 475 anni):
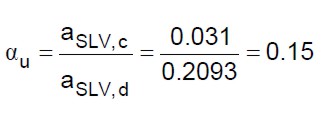 (28)
(28)
Il valore dell’indicatore di rischio dato dalla (28) è stato calcolato tenendo conto dei valori più restrittivi per i coefficienti che compaiono nelle (4). Complicando un po’ l’iter di calcolo si possono ricavare valori meno restrittivi per i coefficienti 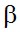 xi,
xi,  xi,
xi,  xi e
xi e  x (analogamente per le direzioni y). Per valutare in modo più accurato i coefficienti sopra riportati occorre valutare la posizione dei baricentri delle masse e delle rigidezze di tutti i piani della struttura. A tale scopo si considerano i maschi murari capaci di traslare solo in testa in modo da poter valutare la rigidezza attraverso la seguente:
x (analogamente per le direzioni y). Per valutare in modo più accurato i coefficienti sopra riportati occorre valutare la posizione dei baricentri delle masse e delle rigidezze di tutti i piani della struttura. A tale scopo si considerano i maschi murari capaci di traslare solo in testa in modo da poter valutare la rigidezza attraverso la seguente:
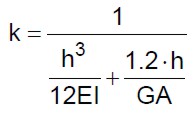 (29)
(29)
dove si indica con h l’altezza del maschio murario, con A l’area della sezione trasversale, con I il momento d’inerzia della sezione trasversale valutato secondo l’asse ortogonale al piano del muro, con E il modulo elastico normale e con G il modulo elastico tangenziale. Il momento d’inerzia si valuta dalla seguente:
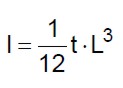 (30)
(30)
I moduli elastici si ricavano dalla tabella 4. Secondo la Circolare 617/2009 occorre assumere come valori di calcolo quelli medi riportati in tabella:

Nelle tabelle 8 si riportano le rigidezze di tutti gli elementi (come per le aree anche le rigidezze vengono moltiplicate per il coseno dell’angolo 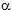 ) e la coordinata dei baricentri interessata dalla direzione (per i maschi in direzione x si riporta la coordinata y, mentre per quelli in direzione y si riporta la coordinata x). La numerazione delle pareti è quella delle figure 4.
) e la coordinata dei baricentri interessata dalla direzione (per i maschi in direzione x si riporta la coordinata y, mentre per quelli in direzione y si riporta la coordinata x). La numerazione delle pareti è quella delle figure 4.
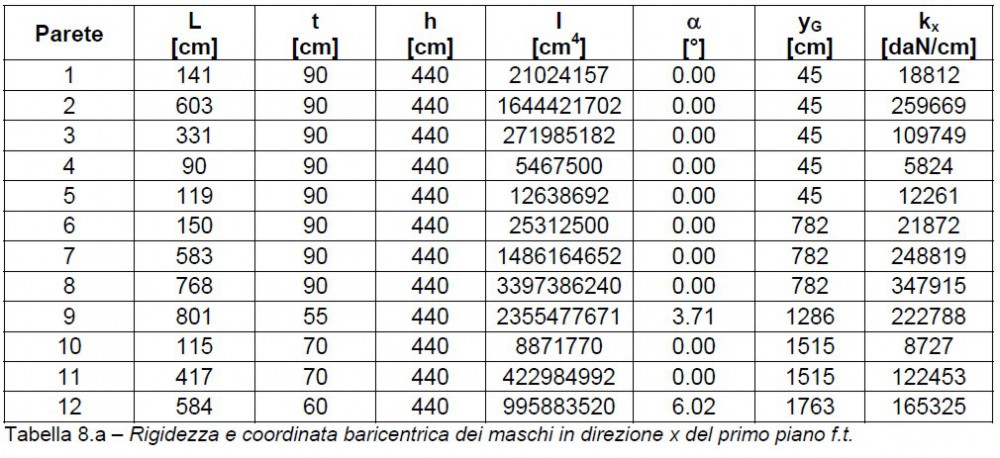
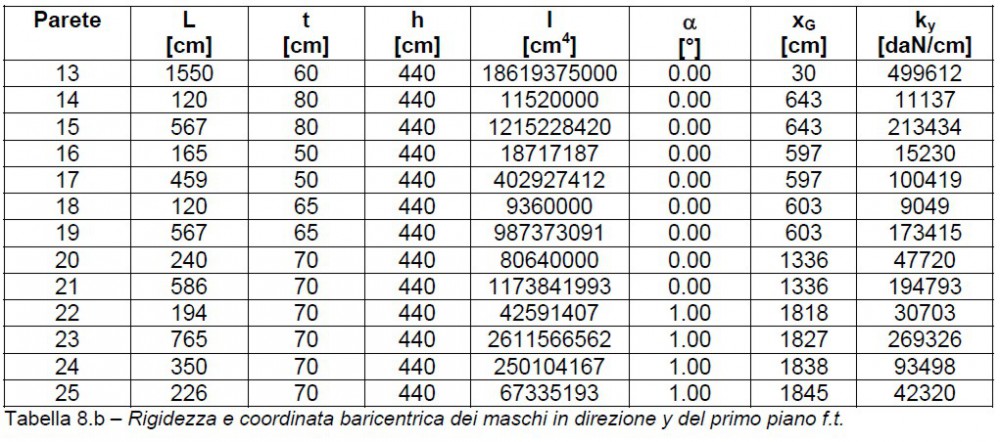
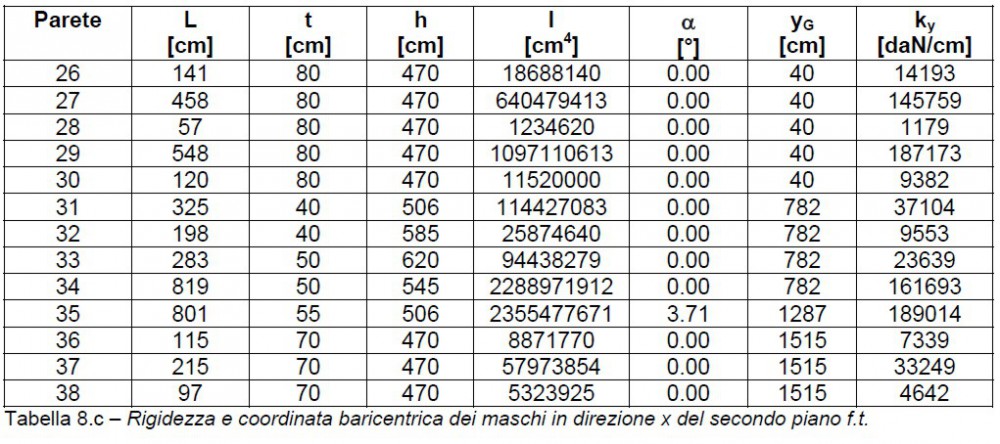
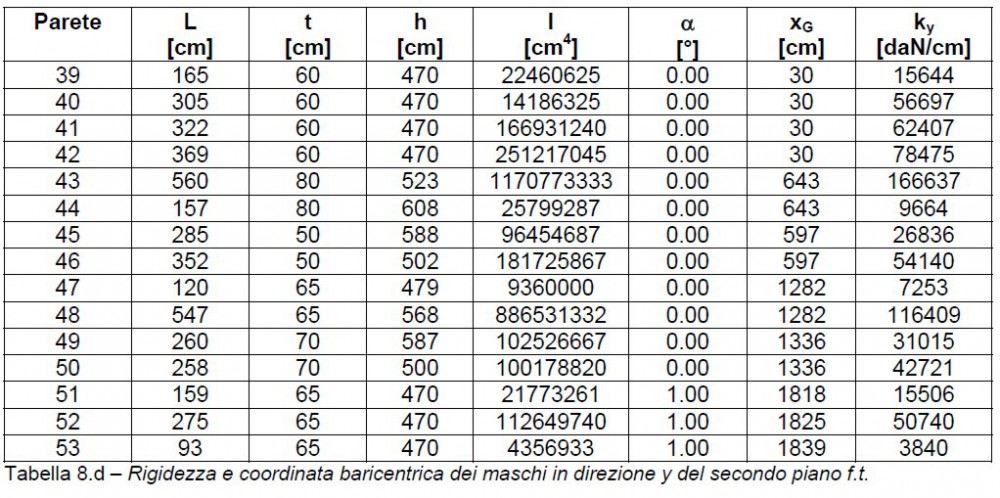
Si riportano nella tabella 9 i baricentri delle rigidezze dei due piani della costruzione.

Per i baricentri delle masse occorre determinare i baricentri di tutti gli elementi con massa (pareti, solai, scale, ecc.) e valutare successivamente quello totale di ogni piano. Nella tabella 10 si riportano i valori dei suddetti baricentri.

Nella tabella 11 si riporta l’eccentricità tra baricentri delle masse e delle rigidezze (si assume in valore assoluto) e la distanza della parete più esterna dal baricentro delle rigidezze (per il primo piano f.t. la distanza dx si ricava dalla parete 3-8 e quella dy dalla parete 7-8, mentre, per il secondo piano f.t. la distanza dx si ricava dalla parete 3-4 e quella dy dalla parete 18-19 – per il riferimento delle pareti vedi figure 1).

Sostituendo i valori numerici sopra calcolati nelle (7) si ottiene:
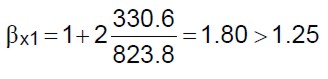 (31.a)
(31.a)
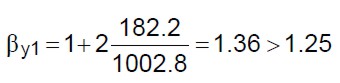 (31.b)
(31.b)
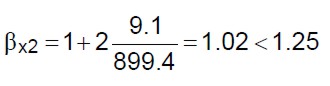 (31.c)
(31.c)
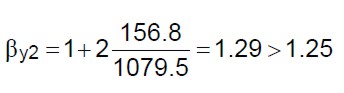 (31.d)
(31.d)
Delle precedenti solo la (31.c) assume il valore minore di 1.25 (valore massimo ammesso), per cui per il coefficiente 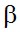 può aumentare solo la resistenza in direzione x del secondo piano f.t.
può aumentare solo la resistenza in direzione x del secondo piano f.t.
I coefficienti  possono essere calcolati in modo più accurato applicando le (8). Le aree con cui calcolare i coefficienti sono riportate nelle tabelle 2. Sostituendo i valori numerici nelle (8) si ottengono i dati riportati nella tabella 12.
possono essere calcolati in modo più accurato applicando le (8). Le aree con cui calcolare i coefficienti sono riportate nelle tabelle 2. Sostituendo i valori numerici nelle (8) si ottengono i dati riportati nella tabella 12.

Ad eccezione di pochi elementi, i maschi murari hanno dimensioni tali da poter ipotizzare la rottura per taglio sia in direzione x che y (vedi figure 4). Ciò consente di attribuire ai coefficienti  il valore 1.
il valore 1.
Per l’assenza di elementi resistenti a trazione, non è possibile considerare le fasce di piano resistenti, per cui i coefficienti  non possono assumere valori migliori di quelli già considerati per valutare l’indicatore di rischio ottenuto dalla (28).
non possono assumere valori migliori di quelli già considerati per valutare l’indicatore di rischio ottenuto dalla (28).
Sostituendo i valori dei coefficienti sopra calcolati nelle (4) si ottiene:
 (32.a)
(32.a)
 (32.b)
(32.b)
 (32.c)
(32.c)
 (32.d)
(32.d)
Sostituendo le (32) nelle (13) si ottiene:
 (33.a)
(33.a)
 (33.b)
(33.b)
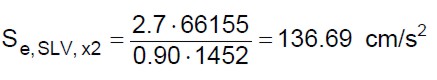 (33.c)
(33.c)
 (33.d)
(33.d)
Tenendo conto della tabella 7 e delle (33) si deduce che il tempo di ritorno per lo stato limite SLV è inferiore a 30 anni. Dalle (3) e dalla (33.d) si ottiene:
 (34)
(34)
L’indicatore di rischio in termini di accelerazioni è dato dalla (35):
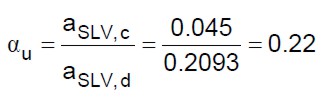 (35)
(35)
Il metodo proposto consente di valutare l’indicatore di rischio della costruzione attraverso una procedura estremamente semplificata. Di contro, il valore ricavato dello stesso indicatore è molto più restrittivo di quello valutato attraverso l’analisi con tecnica più accurata (circa un terzo – vedi tabella 1).
Osservazioni
L’indicatore di rischio calcolato attraverso il metodo semplificato è molto più restrittivo di quello valutato attraverso l’analisi sismica globale. Le motivazioni di questi risultati sono molteplici. Una è legata allo scarso valore di resistenza del materiale. Per analisi di tipo non lineare la normativa consente di adottare come resistenza di calcolo del materiale quella media divisa dal fattore di confidenza (non si divide per il coefficiente di sicurezza). Nel metodo semplificato proposto, i valori medi sono divisi sia dal fattore di confidenza che dal coefficiente di sicurezza. Per metterci nelle stesse condizioni dell’analisi pushover non si divide la resistenza del materiale per il coefficiente di sicurezza. Non tenendo conto di quest’ultimo (assunto pari 2), si ottiene il seguente valore per la resistenza tangenziale:
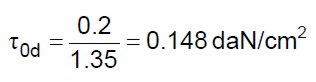 (36)
(36)
Se si assume questo valore anche per il calcolo semplificato (si fa questa ipotesi solo per confrontare le due procedure di calcolo), si ottengono i seguenti risultati:
 (37.a)
(37.a)
 (37.b)
(37.b)
 (38.a)
(38.a)
 (38.b)
(38.b)
 (38.c)
(38.c)
 (38.d)
(38.d)
Sostituendo i valori numerici nelle (13) si ottiene:
 (39.a)
(39.a)
 (39.b)
(39.b)
 (39.c)
(39.c)
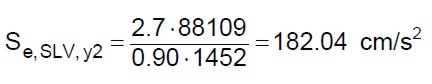 (39.d)
(39.d)
Il valore più basso lo fornisce la (39.d). Dalla tabella 7 si evince che il tempo di ritorno è compreso tra 30 e 50 anni. Dalle (3) e dalla (39.d) si ottiene:
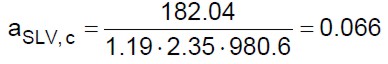 (40)
(40)
L’indicatore di rischio in termini di accelerazioni è dato dalla (41):
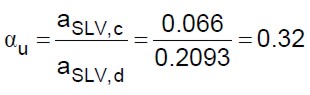 (41)
(41)
Altro fattore che penalizza i risultati è legato alla regolarità della costruzione. Nell’analisi statica non lineare (pushover), poiché non entra in gioco il fattore di struttura, di conseguenza non entra in gioco neanche la regolarità in altezza. Nell’esempio svolto sopra si è assunto che la struttura non è regolare in altezza (dovuto soprattutto per la parte di costruzione crollata al secondo piano). Se si ipotizza la struttura regolare in altezza, il fattore di struttura passa dal valore 2.7 a 3.6. Sostituendo nella (39.d) quest’ultimo valore del fattore di struttura si ottiene (si prende in considerazione solo la relazione (39.d) in quanto quella che fornisce il valore minore):
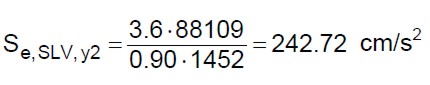 (42)
(42)
Dalla tabella 7 si evince che il tempo di ritorno è compreso tra 72 e 101 anni. L’accelerazione di picco è data dalla seguente:
 (43)
(43)
L’indicatore di rischio in termini di accelerazioni è dato dalla (44):
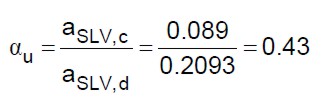 (44)
(44)
Tenendo conto di queste osservazioni (non lecite), l’indicatore di rischio ha un valore di circa 2/3 di quello valutato attraverso l’analisi pushover.
Da quanto visto, il metodo semplificato consente di valutare la resistenza sismica globale della costruzione in modo estremamente semplice, ma nello stesso tempo restituisce risultati molto restrittivi, penalizzandone le prestazioni.
Il metodo può essere valido per una valutazione di massima. Se a seguito del calcolo semplificato si ottiene un indicatore di rischio relativamente basso (minore di 0.5 come nel nostro esempio), è opportuno procedere con tecniche di calcolo più accurate. Se l’indicatore di rischio assume un valore relativamente alto (maggiore di 0.5), la valutazione può essere sufficiente per stabilire che la struttura ha una buona resistenza nei confronti dell’azione sismica.
Si ribadisce ancora che il metodo semplificato in nessun caso può considerarsi esaustivo. A questa verifica occorre affiancare sempre l’analisi dei meccanismi locali (vedi Edificio 1).