Articolo disponibile anche in formato PDF
La progettazione delle sopraelevazioni su edifici esistenti in muratura
Nel presente documento viene svolto un esempio di sopraelevazione in muratura su un edificio esistente in muratura. La progettazione si svolge secondo il metodo semplificato di verifica (costruzioni semplici).
In una prima fase si analizza la struttura esistente per verificare se rientra nella categoria di costruzione semplice.
Affinché un edificio in muratura possa essere considerato costruzione semplice deve rispettare una serie di prescrizioni che riassumiamo in 12 punti (se sono rispettate le 12 condizioni l’edificio è una costruzione semplice).
1 – Struttura esistente
L’edificio esistente è costituito da un solo piano fuori terra, con interpiano pari a 325 cm. È adibito a civile abitazione (carico variabile pari a 200 daN/m2). L’azione sismica di base è riassunta nella tabella 1:
I solai sono di tipo latero-cementizio gettati in opera, per cui possono essere considerati rigidi nel proprio piano. Sulle pareti è presente un cordolo in cemento armato avente larghezza pari allo spessore dei muri sottostanti ed altezza pari a 25 cm. Le fondazioni sono di tipo travi rovesce in cemento armato.
1.1 – Caratteristiche meccaniche della muratura
La muratura esistente può essere assimilata alla categoria Mattoni semipieni e malta cementizia, definita dalla tabella riportata nel punto C8A.2 della Circolare 617/2009, i cui parametri meccanici sono riportati nella tabella 2.
Si assume un livello di conoscenza LC1, per il quale non sono richieste prove distruttive sulla muratura. Per questo livello di conoscenza i parametri meccanici sono totalmente definiti dalla tabella 2, assumendo i valori minimi per le resistenze ed i valori medi per i moduli elastici. Le resistenze caratteristiche devono essere divise per il fattore di confidenza FC = 1.35 e per il coefficiente di sicurezza 
m = 4.2 (valore da assumere solo in caso di costruzioni semplici). In definitiva, i parametri meccanici di calcolo della muratura sono riassunti nella tabella 3.
1.2 – Geometria della struttura
Nelle successive figure viene rappresentata graficamente l’intera struttura attraverso piante e prospetti, in modo da individuare tutti gli elementi di cui è composta. Gli elementi sono riferiti ai fili fissi riportati nelle stesse figure (per individuare gli elementi, tra piante e prospetti, occorre seguire il numero dei fili fissi a cui sono collegati gli estremi). L’insieme degli elaborati consente di definire completamente l’edificio dal punto di vista geometrico.
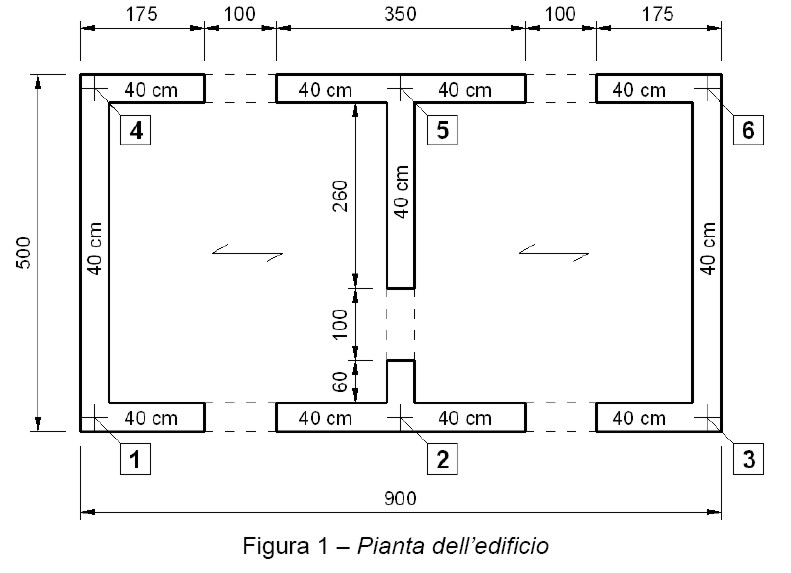
1.3 – Carichi sulla struttura
Sulla struttura gravano i seguenti carichi verticali:
- Peso proprio delle pareti;
- Peso proprio dei cordoli;
- Peso proprio, carico permanente e di esercizio dei solai.
Poiché l’edificio è adibito a civile abitazione, sul tetto grava un carico di esercizio pari a 100 daN/m2 ed uno dovuto alla neve pari ad 80 daN/m2 (totale 180 daN/m2). A seguito della realizzazione del nuovo piano, sullo stesso solaio gravano 200 daN/m2 (civile abitazione).
1.4 – Calcolo della struttura di elevazione
Il calcolo della struttura di elevazione consiste nel controllare che tutte le prescrizioni richieste dalla normativa siano rispettate (prescrizioni relative alle costruzione semplice). Di seguito vengono riportate singolarmente tutte le suddette prescrizioni (riassunte in 12 punti - vedi Le costruzioni semplici in muratura).
1.4.1 – Continuità della muratura fino in fondazione
La struttura portante dell’edificio è costituita da pareti che soddisfano il requisito della continuità fino in fondazione (vedi figure 2).
1.4.2 – Interpiano inferiore a 3.5 m
Il piano dell’edificio esistente ha altezza pari a 3.25 m, inferiore al valore limite pari a 3.5 m (vedi figure 2).
1.4.3 – Numero di piani
Per le costruzioni semplici in muratura ordinaria sono ammessi un massimo di 3 piani. Poiché il nostro edificio è composto da un solo piano (e due a seguito della sopraelevazione), la prescrizione è soddisfatta.
1.4.4 – Rapporto tra i lati dell’edificio in pianta
La lunghezza del lato minore (a) dell’edificio è di 500 cm, mentre quella del lato maggiore (b) è di 900 cm, per cui si ha (vedi figura 1):
Il rapporto tra i lati dell’edificio rispetta i limiti richiesti.
1.4.5 – Snellezza delle pareti
La snellezza 
di una parete è funzione della lunghezza libera di inflessione (h0) e dello spessore (t) della parete stessa. A sua volta, h0 è funzione dell’altezza della parete (h) e del fattore laterale di vincolo (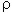
). Il fattore laterale di vincolo può variare da 0 ad 1 per come riportato nella tabella 4.5.IV del punto 4.5.6.2 del D.M. 14/01/2008 in funzione della distanza “a” delle pareti ortogonali che tendono a stabilizzare la parete oggetto di studio. Nella nostra struttura, tutte le pareti hanno altezza pari a h = 300 cm e spessore pari a 40 cm. Se si assume 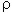= 1 (valore più gravoso) si ottiene:
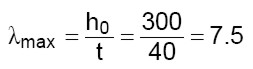(1)
per cui, in definitiva, tutti gli elementi della struttura rispettano il requisito della snellezza (snellezza minore di 12).
1.4.6 – Valore limite del carico variabile (inferiore a 300 daN/m2)
Poiché la struttura è adibita a civile abitazione, dalla tabella 3.1.II del D.M. 14/01/2008 si evince che il carico variabile sui solai è di 200 daN/m2 (carico di esercizio sul solaio a seguito della realizzazione del nuovo piano), minore dei 300 daN/m2 massimi previsti per le costruzioni semplici. Sullo stesso solaio, sono previsti 100 daN/m2 di carico variabile più 80 daN/m2 dovuti al carico da neve (prima di realizzare la sopraelevazione), per un totale di 180 daN/m2. Anche in questo caso il valore è inferiore ai 300 daN/m2 massimi previsti.
1.4.7 – Regolarità della costruzione
L’edificio, per rientrare nella categoria di costruzione semplice, deve essere regolare sia in pianta che in elevazione. È di seguito riportato quanto richiesto dalla normativa affinché l’edificio sia regolare.
1.4.7.1 – Regolarità in pianta
Le prescrizioni relative alla regolarità delle costruzioni sono riportate nel punto 7.2.2 del D.M. 14/01/2008 (vedi Prescrizioni per la regolarità degli edifici in muratura).
1.4.7.1.1 – Verifica delle distribuzioni di masse e rigidezze
La verifica consiste nel controllare che la distanza del baricentro delle masse da quello geometrico sia contenuta in determinati limiti prefissati. Analogamente per il baricentro delle rigidezze.
1.4.7.1.1.1 – Baricentro geometrico
Tenendo conto dell’ingombro degli elementi strutturali di cui è composto l’edificio (vedi figura 1), è possibile determinare agevolmente le coordinate del baricentro geometrico. Nella tabella 4 sono riportate le suddette coordinate. Si assume come origine del sistema di riferimento il punto in basso a sinistra della costruzione.
1.4.7.1.1.2 – Verifica della distribuzione delle masse
La verifica consiste nel controllare che la distanza tra baricentro geometrico e delle masse sia contenuta in determinati limiti prefissati. Assumiamo convenzionalmente tale limite pari al 3% (la distanza tra baricentro delle masse e geometrico in una determinata direzione deve essere contenuta nel 3% della lunghezza dell’edificio nella medesima direzione).
Affinché la prescrizione sia soddisfatta devono essere verificate le seguenti relazioni (vedi Prescrizioni per la regolarità degli edifici in muratura):
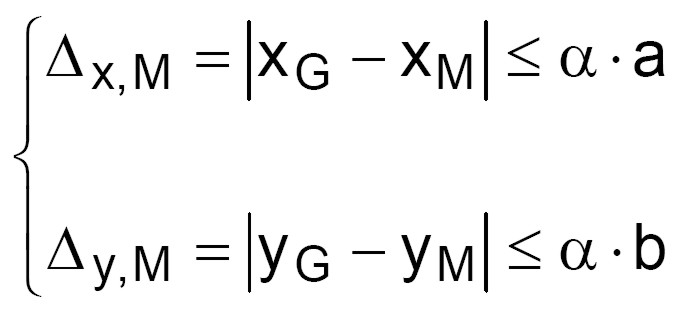(2)
Per avere una corretta valutazione della posizione del baricentro delle masse, occorre conteggiare tutti gli elementi con massa di cui è composta la struttura. Nel nostro caso è composta dai seguenti elementi:
- Pareti in muratura;
- Cordoli in c.a.;
- Solai.
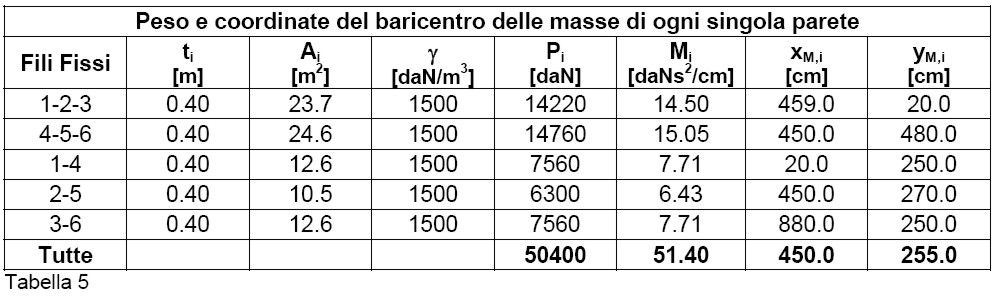
Di seguito si riportano i dati relativi alla valutazione dei baricentri dei suddetti elementi. Naturalmente, le coordinate del baricentro in pianta delle pareti sono state ottenute tenendo conto della posizione delle aperture (vedi tabella 5). Nell’ultima riga della tabella si riportano il peso totale e le coordinate del baricentro di tutte le pareti.
Nella tabella 6 si riportano i dati relativi ai cordoli. Si indica con b la base, con h l’altezza, con L la lunghezza, con Pi il peso, con Mi la massa e con xM,i ed yM,i le coordinate del baricentro in pianta dell’i-esimo cordolo compreso tra i fili fissi indicati. Si indica con il peso specifico del materiale.
Nella tabella 7 si riportano i dati relativi ai solai. Si indica con il peso del solaio per metro quadro (compreso i carichi portati e di esercizio), con Pi il peso totale, con Mi la massa e con xM,i ed yM,i le coordinate del baricentro in pianta dell’i-esimo solaio compreso tra i fili fissi indicati. Il solaio è di tipo latero-cementizio con peso proprio pari 325 daN/m2. Si considerano 100 daN/m2 di permanente portato, 100 daN/m2 di tramezzi (si tiene conto di questi carichi per non ripetere il calcolo a seguito della sopraelevazione) e 200 daN/m2 di esercizio, per un totale di = 725 daN/m2.
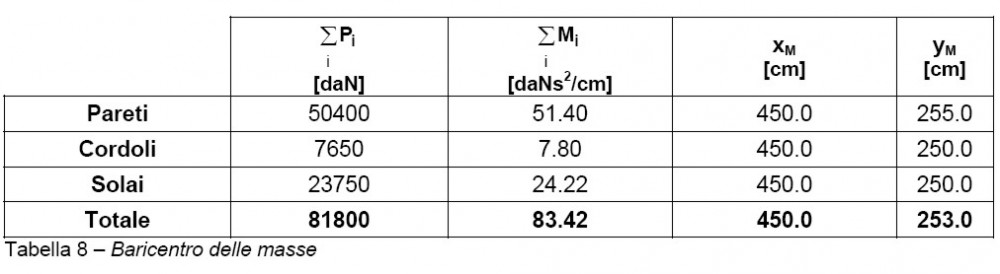
Applicando le note relazioni sul calcolo dei baricentri (vedi Prescrizioni per la regolarità degli edifici in muratura) su tutti i pesi precedentemente calcolati, si ottiene il baricentro delle masse dell’intero piano (vedi tabella 8).
Si assume una percentuale limite pari a 3 (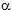
= 0.03) per le distanze tra baricentro geometrico e delle masse:
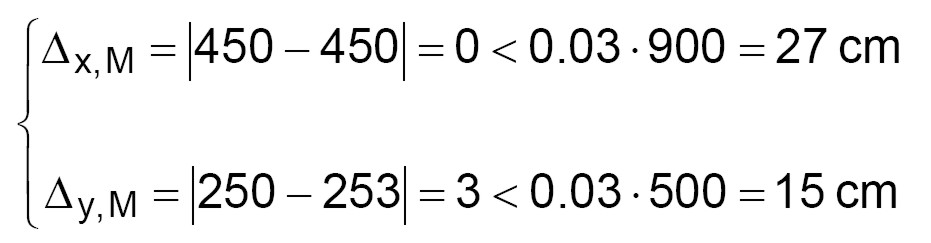(verifica soddisfatta) (3)
Dalle (3) si evince che la verifica è abbondantemente soddisfatta (la distanza tra baricentro delle masse e geometrico è contenuta nei limiti prestabiliti).
1.4.7.1.1.3 – Verifica della distribuzione delle rigidezze
La verifica consiste nel controllare che la distanza tra baricentro geometrico e delle rigidezze sia contenuta in determinati limiti prefissati. Assumiamo convenzionalmente tale limite pari al 3% (la distanza tra baricentro delle rigidezze e geometrico in una determinata direzione deve essere contenuta nel 3% della lunghezza dell’edificio nella medesima direzione).
Per effettuare la verifica della distribuzione delle rigidezze, occorre determinare il baricentro delle stesse rigidezze. Ai maschi murari si attribuisce l’altezza dell’intera parete (dalla fondazione fino al cordolo). Per tutti gli elementi, per come riportato nella tabella 3, il modulo elastico normale assume il valore E = 45500 daN/cm2, mentre quello elastico tangenziale assume il valore G = 11375 daN/cm2. Nella tabella 9 si riportano le rigidezze di ogni singolo maschio murario. Si indica con “Fili fissi” la parete a cui appartiene il maschio murario, con “n° maschio” il numero del maschio murario, con t lo spessore, con l la lunghezza, con kx la rigidezza in direzione x, con ky la rigidezza in direzione y, con xR ed yR il baricentro delle rigidezze del generico maschio murario. Per avere un riferimento grafico di tutti i maschi murari di cui è composto l’edificio consultare le figure 2.
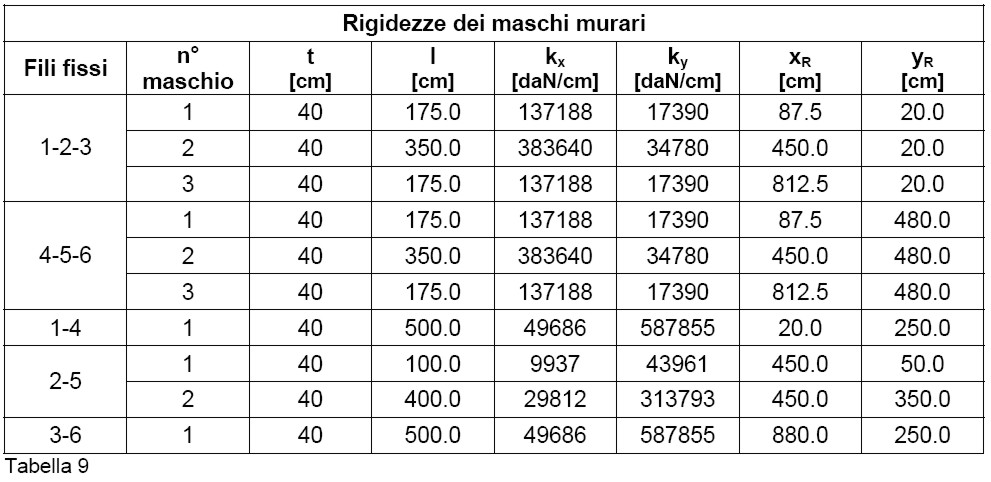
Nella tabella 10 si riportano le rigidezze totali ed i baricentri per ogni piano della struttura. Si indica con kx,i e ky,i la rigidezza dell’i-esimo maschio in direzione x ed y rispettivamente e con xR ed yR le coordinate del baricentro delle rigidezze.
Si assume una percentuale limite pari a 3 (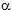 = 0.03) per le distanze tra baricentro geometrico e delle rigidezze:
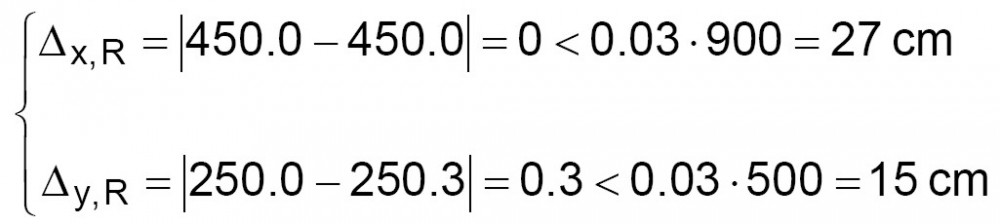(verifica soddisfatta) (4)
Dalle (4) si evince che la verifica è abbondantemente soddisfatta (la distanza tra baricentro delle rigidezze e geometrico è contenuta nei limiti prestabiliti).
Dalle (3) e (4) si evince che l’eccentricità tra baricentro delle rigidezze e delle masse rispetto a quello geometrico non eccede il 3% del corrispondente lato del piano dell’edificio, per cui si può ritenere che rispetta i requisiti relativi alle distribuzioni di masse e rigidezze.
1.4.7.1.2 – Rapporto tra i lati dell’edificio
La prescrizione è stata già verificata nel punto 1.4.4 in condizioni più restrittive.
1.4.7.1.3 – Rientranze e sporgenze in pianta
La struttura non presenta ne sporgenze e ne rientranze per cui la prescrizione è automaticamente soddisfatta.
1.4.7.1.4 – Rigidezza degli orizzontamenti
Poiché gli orizzontamenti della struttura sono di tipo latero-cementizio gettati in opera, possono essere considerati rigidi nel proprio piano.
1.4.7.2 – Regolarità in elevazione
Essendo l’edificio esistente costituito da un solo piano, la regolarità in elevazione è automaticamente soddisfatta.
1.4.8 – Sistemi di pareti
Le prescrizioni seguenti sono quelle riportate nel punto 7.8.5.1 del D.M. 14/01/2008, specifico per le costruzioni semplici (vedi punto 8 di Le costruzioni semplici in muratura).
In direzione X, si prendono come i due sistemi di pareti quelle composte dalle pareti “1–2–3” e “4–5–6” che rappresentano le due pareti più distanti nella direzione considerata (distanza pari al 100% della lunghezza della struttura nella direzione ortogonale a quella delle pareti). Rimane da verificare che la lunghezza dei maschi resistenti a sisma sia almeno pari al 50% della lunghezza della costruzione nella medesima direzione. I maschi idonei a resistere all’azione sismica possono essere ricavati graficamente dalle figure 2. Analogamente, per la direzione Y, si prendono come i due sistemi di pareti, la “1–4” e la “3–6”. Anche in questo caso la loro distanza e pari al 100% della dimensione dell’edificio nella direzione ortogonale a quella delle pareti.
Prima di procedere occorre verificare quali sono i maschi murari che rispettano i requisiti imposti dalla tabella 7.8.II del D.M. 14/01/2008 (vedi tabella 11).
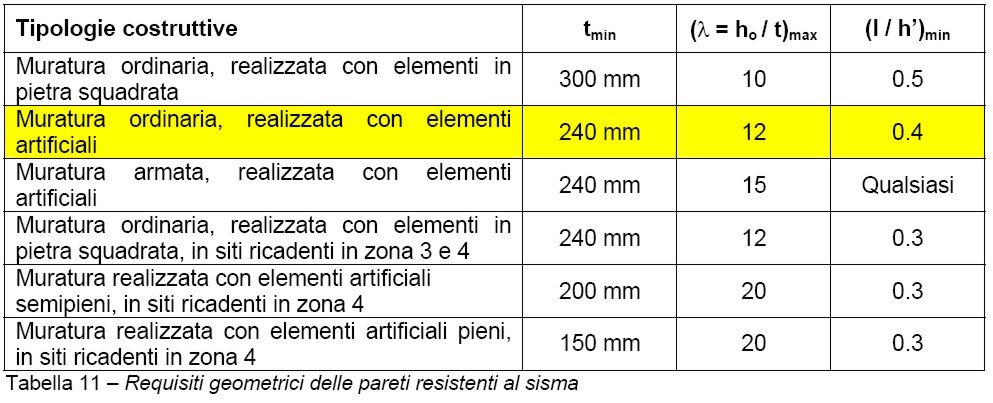
La prescrizione relativa allo spessore è rispettata per tutti gli elementi in quanto tutte le pareti hanno spessore pari a 40 cm (maggiore dei 24 cm minimi richiesti), la snellezza è minore di 12 (vedi punto 1.4.5) ed il rapporto tra lunghezza dell’elemento ed altezza del foro adiacente è maggiore di 0.4. Dimostriamo quest’ultima condizione sul primo maschio murario della parete “1-2-3” (maschio con condizioni più gravose - lunghezza (l) pari a 175 cm ed altezza (h’) dell’apertura adiacente pari a 210 cm):
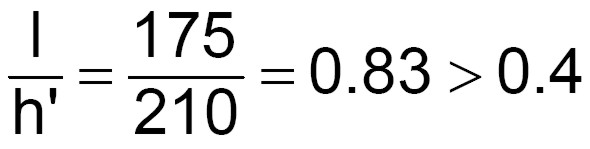(5)
Tutti gli elementi di cui è composta la struttura rispettano le prescrizioni della tabella 11 per cui idonei a resistere all’azione sismica.
Verifica della somma delle lunghezze dei maschi murari
Parete 1–2–3
(verifica soddisfatta)
Parete 4–5–6
(verifica soddisfatta)
Parete 1–4
(verifica soddisfatta)
Parete 3–6
(verifica soddisfatta)
1.4.9 – Carico verticale su pareti idonee alla resistenza sismica
Occorre verificare che almeno il 75% dei carichi sia portato da elementi idonei alla resistenza sismica. Poiché si è dimostrato nel punto 1.4.8 che tutti gli elementi sono idonei, la prescrizione risulta essere automaticamente soddisfatta.
1.4.10 – Distanza tra pareti parallele
Per edifici in muratura ordinaria, la distanza tra le pareti non deve eccede i 7 m. Come è possibile vedere dalla figura 1, tale prescrizione è ampiamente soddisfatta. In direzione X la massima distanza tra le pareti è di 4.60 m, mentre la massima distanza in direzione Y è di 4.30 m.
1.4.11 – Area di muratura
Dalla tabella 7.8.III del D.M. 14/01/2008 si ottiene la percentuale di muratura portante di cui deve essere dotata la struttura. Possono essere computati solo gli elementi che rispettano le prescrizioni della tabella 7.8.II dello stesso D.M. (nel nostro esempio sono idonei tutti gli elementi). Poiché si ha (vedi tabella 1):
e tenendo conto del numero di piani di cui è composta la struttura (2 nel nostro caso considerando anche il piano di sopraelevazione), ne consegue che è necessaria una percentuale di muratura pari a 5.5 (vedi tabella 12).
Nelle successive tabelle si calcola l’area di muratura in direzione X ed Y.
La superficie lorda della costruzione è:
(6)
Direzione X
(verifica soddisfatta)
Direzione Y
(verifica soddisfatta)
1.4.12 – Tensione sulla muratura
Rimane da verificare la tensione sulla muratura secondo la relazione 7.8.1 del D.M. 14/01/2008. La tensione di calcolo a compressione della muratura si ottiene dalla tabella 3 e vale fd = 8.82 daN/cm2. Lo sforzo normale alla base della costruzione si ottiene dalla tabella 8 e vale N = 81800 daN. La superficie totale di muratura (al netto delle aperture) è pari a A = 102400 cm2. In definitiva si ha:
(verifica soddisfatta) (7)
Fino a questo punto dell’esempio è stata analizzata la costruzione esistente con lo scopo di dimostrare che rientra nella tipologia di costruzioni semplici secondo cui la normativa consente l’approccio di verifica semplificato.
2 – Progetto del piano di sopraelevazione (prima ipotesi progettuale)
Si procede con la progettazione del nuovo piano. In una prima fase della progettazione si ipotizza il nuovo piano con le stesse caratteristiche geometriche in termini di interpiano e distribuzioni delle aperture di quello esistente. Si assume per la muratura uno spessore pari a 30 cm (si ricorda che quella al piano inferiore ha spessore pari a 40 cm). Quanto appena detto ci garantisce l’esito positivo della verifica per molti dei punti già verificati per l’edificio ad un solo piano.
Il solaio di nuova costruzione è di tipo latero-cementizio con le stesse caratteristiche di quello esistente. Il peso proprio è pari a 325 daN/m2. Si considerano inoltre 100 daN/m2 di permanente, 100 daN/m2 di esercizio e 80 daN/m2 di carico da neve (peso complessivo pari a 605 daN/m2)
Oltre ai carichi considerati nel punto 1.3 occorre tenere conto del carico dovuto al parapetto sul terrazzo (alto 100 cm), valutato 120 daN/m.
2.1 – Geometria della struttura
Nelle successive figure viene rappresentata graficamente l’intera struttura attraverso piante e prospetti, in modo da individuare tutti gli elementi di cui è composta.
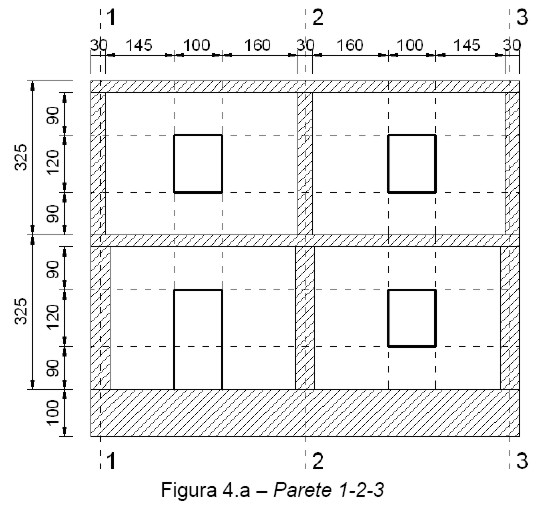
2.2 – Caratteristiche dei materiali
Per la muratura di nuova costruzione si utilizza un blocco con spessore pari a 30 cm. La resistenza caratteristica del blocco (fbk) è pari ad 80 daN/cm2 e si assume una malta di categoria M10. Il peso specifico della muratura si assume pari a 1400 daN/m3. Dalla tabella riportata nel punto 11.10.3.1.2 del D.M. 14/01/2008, si ottiene la resistenza caratteristica a compressione (fk) della muratura pari a 46.6 daN/cm2. I moduli elastici normale (E) e tangenziale (G) sono ricavabili in funzione della resistenza caratteristica a compressione della muratura. La tensione di calcolo (fd) si ottiene da quella caratteristica dividendo per il coefficiente di sicurezza 4.2. In definitiva, le caratteristiche meccaniche della muratura di nuova costruzione sono riassunte nella tabella 15.
2.3 – Calcolo della struttura di elevazione con sopraelevazione
Come per il caso della struttura costituita da un solo piano, la verifica consiste nel controllare tutte le prescrizioni richieste dalla normativa affinché un edificio possa essere considerato costruzione semplice.
2.3.1 – Continuità della muratura fino in fondazione
La struttura portante dell’edificio è costituita da pareti che soddisfano il requisito della continuità fino in fondazione (vedi figure 4).
2.3.2 – Interpiano inferiore a 3.5 m
Il piano di nuova costruzione ha altezza pari a 3.25 m (come quello esistente), inferiore al valore limite pari a 3.5 m (vedi figure 4).
2.3.3 – Numero di piani
L’aggiunta del nuovo piano porta a due quelli totali della costruzione, inferiore al limite massimo di tre piani per le costruzioni semplici.
2.3.4 – Rapporto tra i lati dell’edificio in pianta
Prescrizione già verificata nel punto 1.4.4.
2.3.5 – Snellezza delle pareti
La snellezza degli elementi del nuovo piano cambia in quanto cambia lo spessore, passando da 40 cm a 30 cm. Per questi elementi la snellezza è pari a:
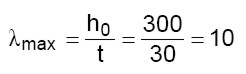(8)
minore di 12 (verifica soddisfatta).
2.3.6 – Valore limite del carico variabile (inferiore a 300 daN/m2)
Poiché la struttura è adibita a civile abitazione, dalla tabella 3.1.II del D.M. 14/01/2008 si evince che il carico variabile sui solai è di 200 daN/m2 (carico di esercizio sul primo solaio a seguito della realizzazione del nuovo piano), minore dei 300 daN/m2 massimi previsti per le costruzioni semplici. Sul solaio di copertura sono previsti 100 daN/m2 di carico di esercizio più 80 daN/m2 dovuti al carico da neve, per un totale di 180 daN/m2. Anche in questo caso il valore è inferiore ai 300 daN/m2 massimi previsti.
2.3.7 – Regolarità della costruzione
Si verifica la regolarità dell’edificio, sia in pianta che in altezza.
2.3.7.1 – Regolarità in pianta
Poiché la distribuzione in pianta degli elementi è simile a quella del piano inferiore, si ritiene che anche il piano superiore sia regolare in pianta (la differenza dello spessore delle pareti può portare a piccole differenze della posizione dei baricentri rispetto al piano inferiore, ma non tali da compromettere la regolarità in pianta).
2.3.7.2 – Regolarità in elevazione
Poiché l’edificio è costituito da due piani, occorre controllare le prescrizioni richieste per la regolarità in altezza (prescrizioni non prese in considerazione per la sola parte esistente dell’edificio in quanto costituita da un solo piano).
2.3.7.2.1 – Continuità dei sistemi resistenti in elevazione
Tutti gli elementi presentano la continuità fino in fondazione (vedi figure 4) per cui la prescrizione si ritiene soddisfatta.
2.3.7.2.2 – Variazione di masse e rigidezze
Occorre verificare che la variazione di massa e rigidezza tra i diversi piani dell’edificio rientri in determinati limiti prestabiliti (vedi Prescrizioni per la regolarità degli edifici in muratura).
2.3.7.2.2.1 – Variazione delle masse
Le masse totali del primo piano della struttura sono state calcolate nel paragrafo 1.4.7.1.1.2 e riportate nell’ultima riga della tabella 8. Nella tabella 16 si riportano quelle relative al secondo piano (rispetto al piano esistente varia lo spessore del muro, la larghezza dei cordoli ed i carichi di esercizio sul solaio di copertura. Inoltre, occorre computare anche il carico dovuto ai parapetti. In questo contesto, visto lo scopo didattico dell’esempio, non si tiene conto di eventuali carichi dovuti alle scale).
Affinché la verifica sia soddisfatta, la variazione di massa tra due piani contigui deve essere contenuta nel 25% (i dati della tabella 16 sono da confrontare con quelli della tabella 8).
Variazione di massa tra i due piani
(9)
La differenza delle masse tra i due piani è contenuta nel 25%.
2.3.7.2.2.2 – Variazione delle rigidezze
Le rigidezze dei singoli elementi del primo piano f.t. sono state determinate nel punto 1.4.7.1.1.3 (vedi tabella 9). Per confrontare le rigidezze dei due piani occorre definire anche quelle del nuovo piano (diverse da quelle del piano inferiore per la qualità del materiale e per la differenza dello spessore delle pareti). Si riportano nella tabella 17 le rigidezze del nuovo piano.
Nella tabella 18 si riportano le rigidezze per ogni piano e per entrambe le direzioni principali della struttura (per la rigidezza in direzione X si considerano solo le pareti in direzione X ed analogamente per la rigidezza in direzione Y).
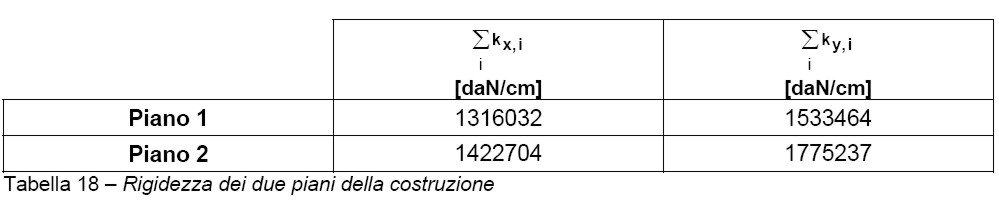
Nei casi in cui la rigidezza del piano superiore è maggiore di quella del piano inferiore, l’incremento deve essere contenuto nel 10%, mentre se minore, la riduzione deve essere contenuta nel 30%. Nel nostro caso, la rigidezza del piano superiore aumenta sia in direzione X che in direzione Y (la variazione di rigidezza deve essere contenuta nel 10%).
Variazione di rigidezza in direzione X tra i due piani
(verifica soddisfatta) (10.a)
Variazione di rigidezza in direzione Y tra i due piani
(verifica non soddisfatta) (10.b)
La variazione delle rigidezze è rispettata per la direzione X e non rispettata per la direzione Y. Sotto queste condizioni la costruzione non può essere considerata costruzione semplice, per cui non è possibile applicare il metodo semplificato di verifica. Per procedere secondo questo metodo di verifica occorre effettuare qualche modifica della costruzione.
3 – Progetto del piano di sopraelevazione (seconda ipotesi progettuale)
Per far rientrare la verifica relativa alla differenza di rigidezze tra i due piani occorre ridurre quella del piano di nuova costruzione. Per raggiungere lo scopo, si può procedere diminuendo la rigidezza del materiale attraverso l’utilizzo di blocchi con caratteristiche meccaniche più scadenti (con modulo elastico minore). Si può ridurre lo spessore delle pareti in quanto il valore minimo consentito è di 24 cm (in quest'ultimo caso si rischia di non rientrare nel limite del 25% della variazione della massa tra i due piani – vedi relazione (9) nel punto 2.3.7.2.2.1). In alternativa si può ridurre la rigidezza aumentando l’interpiano della costruzione. Nella prima ipotesi progettuale si è assunto un interpiano pari a 325 cm. Per le costruzioni semplici è ammesso un interpiano pari a 350 cm, per cui rispetto al caso precedente si incrementa l’altezza di 25 cm.
3.1 – Calcolo della struttura di elevazione con sopraelevazione
Si rielabora la struttura secondo questa nuova geometria.
3.1.1 – Continuità della muratura fino in fondazione
Vedi punto 2.3.1.
3.1.2 – Interpiano inferiore a 3.5 m
Il piano di nuova costruzione ha altezza pari a 3.50 m, uguale al valore limite ammesso.
3.1.3 – Numero di piani
Vedi punto 2.3.3.
3.1.4 – Rapporto tra i lati dell’edificio in pianta
Vedi punto 1.4.4.
3.1.5 – Snellezza delle pareti
Rispetto a quanto calcolato nel punto 2.3.5 aumenta l’interpiano per cui aumenta la snellezza degli elementi:
(11)
minore di 12 (verifica soddisfatta).
3.1.6 – Valore limite del carico variabile (inferiore a 300 daN/m2)
Vedi punto 2.3.6.
3.1.7 – Regolarità della costruzione
Di seguito si verifica la regolarità dell’edificio, sia in pianta che in altezza.
3.1.7.1 – Regolarità in pianta
Vedi punto 2.3.7.1.
3.1.7.2 – Regolarità in elevazione
Nella prima ipotesi progettuale (altezza dell’interpiano pari a 325 cm) risultava negativa la verifica della regolarità in altezza. Si riesegue la verifica tenendo conto di questa nuova altezza dell’interpiano (pari a 350 cm).
3.1.7.2.1 – Continuità dei sistemi resistenti in elevazione
Vedi punto 2.3.7.2.1.
3.1.7.2.2 – Variazione di masse e rigidezze
Occorre verificare che la variazione delle masse e delle rigidezze tra i due piani dell’edificio rientri in determinati limiti prefissati.
3.1.7.2.2.1 – Variazione delle masse
Nella tabella 19 si riportano le masse relative al secondo piano con altezza dell’interpiano pari a 350 cm.
Affinché la verifica sia soddisfatta, la variazione di massa tra due piani contigui deve essere contenuta nel 25% (i dati della tabella 19 sono da confrontare con quelli della tabella 8).
Variazione di massa tra i piani
(12)
La differenza delle masse tra i due piani è contenuta nel 25%.
3.1.7.2.2.2 – Variazione delle rigidezze
Si ricalcola la rigidezza degli elementi del secondo piano f.t. tenendo conto dell’altezza degli elementi in muratura pari a 325 cm. Nella tabella 20 se ne riportano i valori.
Nella tabella 21 si riportano le rigidezze per ogni piano e per entrambe le direzioni principali della struttura (per la rigidezza in direzione X si considerano solo le pareti in direzione X ed analogamente per le pareti in direzione Y).
La rigidezza del piano superiore diminuisce per la direzione X (si consente una riduzione del 30%) ed aumenta per la direzione Y (si consente un aumento del 10%).
Variazione di rigidezza in direzione X tra i due piani
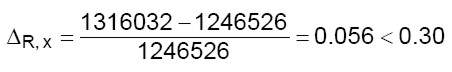(13.a)
Variazione di rigidezza in direzione Y tra i due piani
(13.b)
La variazione delle rigidezze tra i piani è rispettata sia per la direzione X che per quella Y.
3.1.7.2.3 – Rientranze in elevazione
L’edificio non presenta alcuna rientranza in elevazione.
3.1.8 – Sistemi di pareti
Per i sistemi di pareti valgono le stesse considerazioni viste nel punto 1.4.8.
3.1.9 – Carico verticale su pareti idonee alla resistenza sismica
Tutti gli elementi rispettano le prescrizioni della tabella 7.8.II del D.M. 14/01/2008 per cui la prescrizione è automaticamente soddisfatta.
3.1.10 – Distanza tra pareti parallele
Vedi punto 1.4.10.
3.1.11 – Area di muratura
L’area di muratura del primo piano è sufficiente (dimostrato nel punto 1.4.11). Occorre dimostrare che anche l’area di muratura del secondo piano f.t. rispetti le percentuali della tabella 12 (5.5%). Nelle successive tabelle si calcola l’area di muratura in direzione X ed Y del secondo piano f.t.
La superficie lorda della costruzione è:
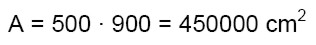(14)
Direzione X
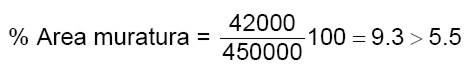(verifica soddisfatta)
Direzione Y
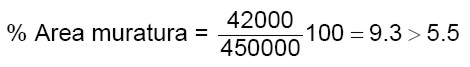(verifica soddisfatta)
3.1.12 – Tensione sulla muratura
Rimane da verificare la tensione sulla muratura secondo la relazione 7.8.1 del D.M. 14/01/2008. Tale verifica deve essere effettuata alla base di ogni piano. La tensione di calcolo a compressione della muratura esistente è stata valutata nel punto 1.1 (tabella 3), mentre quella della muratura del nuovo piano è stata valutata nel punto 2.2 (tabella 15). Lo sforzo normale alla base del secondo piano si ricava dalla tabella 19 e vale N2 = 70084 daN, mentre lo sforzo normale alla base del primo piano si ottiene sommando N2 al peso riportato nella tabella 8 (N1 = 81800 + 70084 = 151884 daN). L’area di muratura del primo piano è stata valutata nel punto 1.4.12 (A1 = 102400 cm2), mentre quella del secondo piano vale A2 = 78600 cm2 (al netto delle aperture).
Piano 1
(15.a)
Piano 2
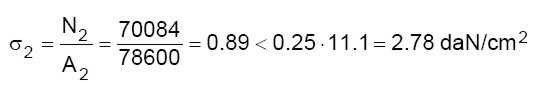(15.b)
L’edificio costituito da un piano esistente e da uno di nuova costruzione rientra nella categoria delle costruzioni semplici, consentendo la progettazione attraverso il metodo di verifica semplificato.
Si riportano nelle figure 5 la geometria definitiva della costruzione (la pianta è quella di figura 3).
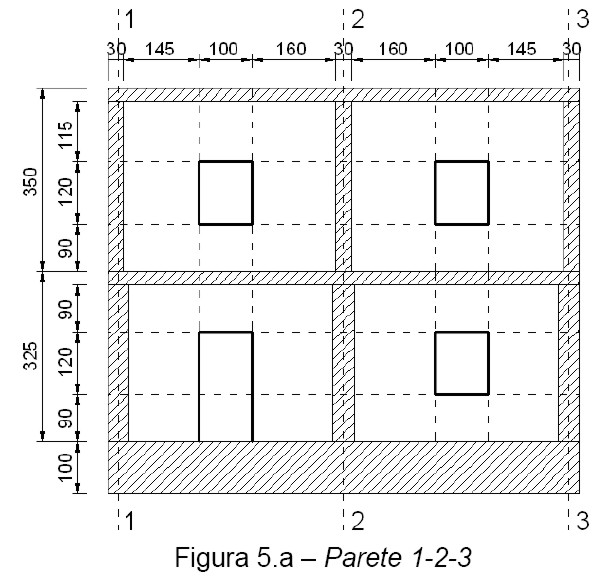
4 – Osservazioni
In questo documento è stato sviluppato un esempio di sopraelevazione in muratura su un edificio esistente in muratura attraverso il metodo semplificato di verifica. Ciò è stato possibile per la semplicità della costruzione. Fondamentale è stata la geometria dell’edificio (caratteristiche pressoché simmetriche che agevolano la regolarità della costruzione) e la qualità del materiale esistente. In particolare, il valore relativamente alto del modulo elastico ha consentito di rientrare nel 10% di differenza tra le rigidezze dei due piani. Se per esempio il materiale del piano esistente fosse quello definito dalla Circolare 627/2009 come pietrame disordinato il cui modulo elastico medio è 8700 daN/cm2, probabilmente la prescrizione della variazione delle rigidezze tra i piani non sarebbe soddisfatta. Se si tenta di abbassare la rigidezza del nuovo piano riducendo lo spessore dei muri (massa inferiore), si finisce per non soddisfare la prescrizione relativa alla variazione delle masse tra i piani che deve essere contenuta nel 25%. In questi casi, la soluzione è quella di progettare il nuovo piano attraverso i metodi di verifica più complessi previsti dalla normativa, prestando attenzione che siano tutte soddisfatte (condizione di adeguamento).
Nel testo riportato in bibliografia sono riportati esempi di sopraelevazione più complessi, progettate sia attraverso la tecnica di verifica semplificata che attraverso quella che prevede il calcolo strutturale più complesso e dettagliato.