 Articolo disponibile anche in formato PDF
Articolo disponibile anche in formato PDF
A seguito dei recenti eventi sismici si è parlato molto di edifici in muratura, sia di quelli che purtroppo sono crollati che di quelli che per fortuna non hanno subito particolari danni, consentendo alle persone di mettere in salvo la propria vita. Molto si è detto di alcuni dispositivi, come per esempio i tiranti, che consentono di aumentare la resistenza delle costruzioni. Naturalmente, i tiranti non sono la panacea di tutti i mali, ma di sicuro consentono alle costruzioni (e soprattutto alle persone che le abitano) di avere qualche speranza in più di sopravvivenza nei confronti degli eventi sismici. In questo articolo, cercheremo di fare alcune considerazioni di carattere numerico (seguendo quanto riportato dalla normativa attraverso tecniche di calcolo semplificate) su una struttura di modeste dimensioni (edificio con caratteristiche simili a migliaia diffusi su tutto il territorio nazionale).
Recenti studi hanno messo in evidenza che gli edifici in muratura sono più vulnerabili nei confronti dei meccanismi locali (perdita di equilibrio di parti di esse) rispetto a stati di crisi di tipo globale. Ciò è stato riscontrato anche nei recenti eventi sismici. Moltissimi crolli sono stati innescati dalla perdita di equilibrio di qualche elemento.
Per conferma di quanto sopra detto, si riporta di seguito un esempio di edificio in muratura, analizzato secondo la tecnica dei meccanismi locali.
Esempio di calcolo
Si valuti la vulnerabilità sismica della struttura riportata in figura 1 secondo la tecnica dei meccanismi locali (ribaltamento semplice, flessione verticale ed orizzontale).
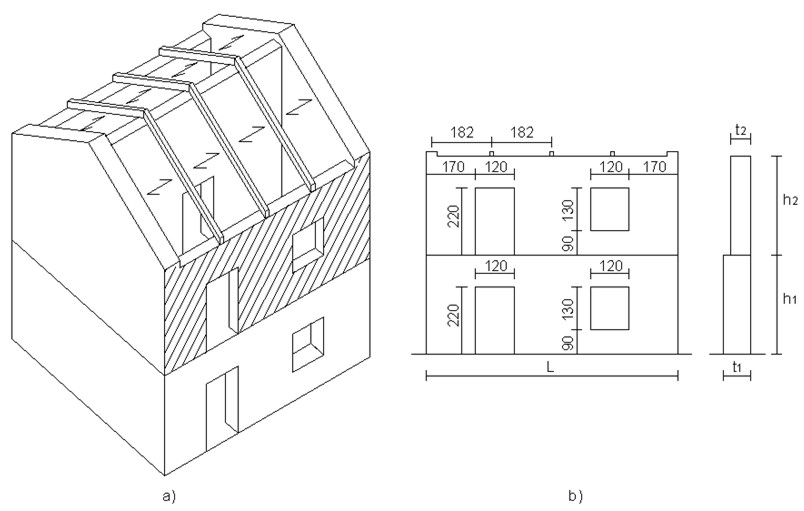
Figura 1 – Struttura tratta dal testo [1] riportato in bibliografia
Dati
- Lunghezza delle pareti (L) = 780 cm
- Larghezza dell’edificio = 500 cm
- Altezza della parete per ogni piano (h1, h2) = 320 cm
- Altezza della parete di colmo (entrambi i piani) = 790 cm
- Spessore della parete del piano terra (t1) = 50 cm
- Spessore della parete del primo piano (t2) = 40 cm
- Spessore delle pareti ortogonali (to) = 50 cm
- Peso totale del sistema tetto = 300 daN/m2
- Peso totale del solaio al primo impalcato = 650 daN/m2
- Suolo di fondazione = B
- Categoria topografica = T1
- Livello di conoscenza = LC1
- Muratura in mattoni pieni e malta di calce
- Coefficiente di sicurezza (
 m) = 2
m) = 2
- Malta di buona qualità
- Edificio ubicato nel comune di Norcia.
Soluzione
Per non allungare notevolmente l’esempio si analizza solo la parete tratteggiata riportata in figura 1. A tale fine si affronta l’analisi della struttura seguendo tecniche semplificate di calcolo (affrontabili anche senza l’ausilio di elaboratori elettronici).
Note le coordinate geografiche del sito e le caratteristiche del terreno di fondazione, è possibile valutare l’azione sismica di riferimento (valutata attraverso il software STR) con la quale analizzare la struttura (vedi figura 2). Nelle tabelle 1 e 2 vengono riassunti i parametri che definiscono l’azione sismica.
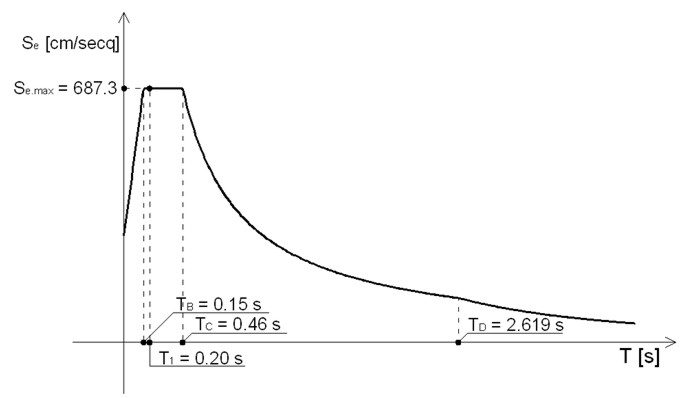
Figura 2 – Spettro elastico di riferimento

Tabella 1 – Dati che definiscono l’azione sismica

Tabella 2 – Dati che definiscono lo spettro di progetto
Il periodo proprio della struttura può essere valutato in modo semplificato attraverso la seguente:
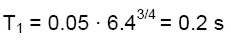 (1)
(1)
Entrando nello spettro con il periodo T1 si ottiene l’accelerazione sismica con la quale effettuare le verifiche:
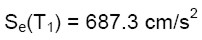 (2)
(2)
In questo contesto si effettua l’analisi cinematica lineare. Secondo quanto riportato dalla normativa, l’esito della verifica è soddisfatto se sono soddisfatte le seguenti (la (3.b) è da considerare solo se la parte di struttura interessata dal meccanismo si trova a quota superiore rispetto a quella della fondazione):
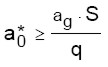 (3.a)
(3.a)
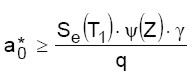 (3.b)
(3.b)
1. Stato di fatto
In questa prima fase si analizza la parete priva di interventi.
Ribaltamento semplice
Il ribaltamento semplice di una parete si verifica generalmente per la scarsa connessione tra due pareti ortogonali ed in assenza di elementi resistenti a trazione (cordoli, tiranti, FRP, ecc.). Esempi di meccanismo a ribaltamento semplice sono riportati in figura 3.
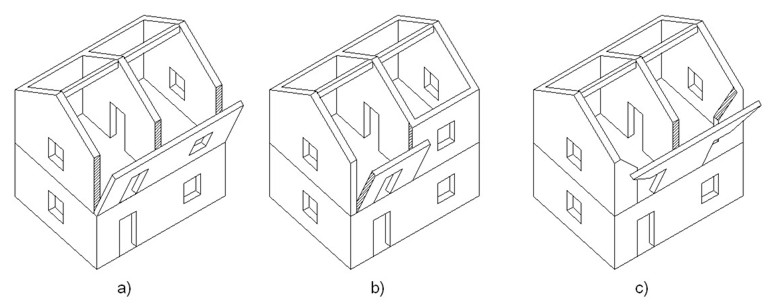
Figura 3 – Esempi di meccanismo a ribaltamento semplice
Nel nostro esempio, la parete oggetto di studio è quella riportata in figura 1. Si ipotizza la cerniera cinematica in corrispondenza del solaio del primo piano f.t. (quota a 320 cm). I carichi che gravano sulla parete sono:
- Il peso proprio della parete (W2);
- Il carico verticale del tetto (si considera come la somma dei carichi dovuti ai tre travetti: Ps2 = Ps2,1 + Ps2,2 + Ps2,3) applicato nel piano medio della parete. Per la particolare disposizione dei vincoli, il tetto non si considera spingente;
- Azioni inerziali dovute alla massa della parete ed a quella del tetto (
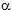 0 ∙ W2,
0 ∙ W2, 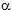 0 ∙ Ps2).
0 ∙ Ps2).
Per risolvere il meccanismo occorre calcolare tutte le grandezze che entrano in gioco nelle (3) (poiché la cerniera cinematica è a quota maggiore rispetto a quella della fondazione, occorre risolvere anche la (3.b)). Tutte le grandezze al secondo membro delle (3) sono facilmente valutabili (per il significato dei simboli si rimanda ai testi citati in bibliografia). Dalle (3) si ottiene:
 (4.a)
(4.a)
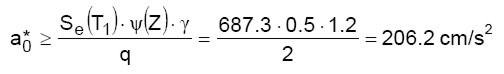 (4.b)
(4.b)
Dalle (4) si deduce che, affinché l’esito della verifica sia positivo, l’accelerazione spettrale di attivazione del meccanismo (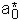 ) deve essere maggiore di a*0,min = 206.2 cm/s2. La suddetta accelerazione si ottiene dalla seguente:
) deve essere maggiore di a*0,min = 206.2 cm/s2. La suddetta accelerazione si ottiene dalla seguente:
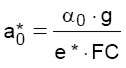 (5)
(5)
Per definire la (5) occorre definire il moltiplicatore dei carichi orizzontali 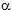 0 e quindi occorre valutare le azioni che gravano sulla parete e le loro posizioni (vedi tabella 3 e figura 4).
0 e quindi occorre valutare le azioni che gravano sulla parete e le loro posizioni (vedi tabella 3 e figura 4).

Tabella 3 – Carichi interessati dal meccanismo
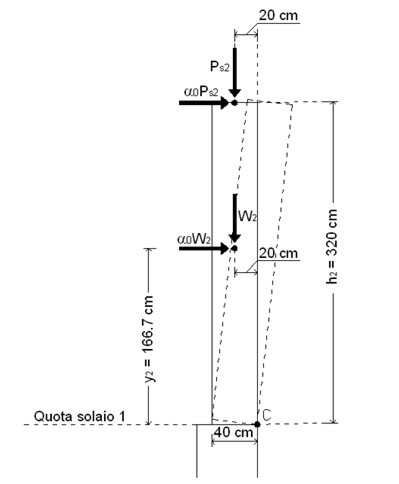
Figura 4 – Posizione dei carichi
Dall’equilibrio alla rotazione intorno alla cerniera cinematica C si ottiene il seguente valore del moltiplicatore di attivazione del meccanismo:
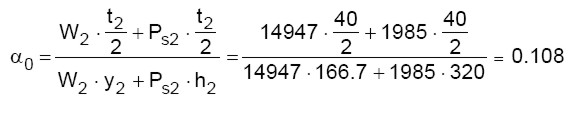 (6)
(6)
La massa partecipante M* vale:
 (7)
(7)
La frazione di massa partecipante vale:
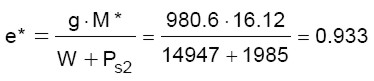 (8)
(8)
Note tutte le quantità, dalla (5) è possibile calcolare l’accelerazione spettrale di attivazione del meccanismo (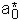 ):
):
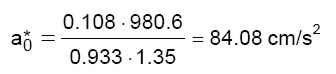 (9)
(9)
In definitiva si ottiene:
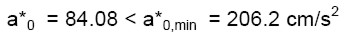 (10)
(10)
per un coefficiente di sicurezza pari a (nell’espressione successiva il pedice “RS” indica il meccanismo di ribaltamento semplice mentre il pedice “a” indica ante operam):
 (verifica non soddisfatta) (11)
(verifica non soddisfatta) (11)
Dalla (11) si deduce che la resistenza della parete all’azione sismica (ribaltamento semplice) è di circa il 41% di quella prevista da normativa.
Flessione verticale
Il meccanismo a flessione verticale è abbastanza comune negli edifici in muratura e generalmente si manifesta quando la parete è ben vincolata agli estremi (superiore ed inferiore) e priva di qualsiasi connessione efficace nelle quote intermedie della parete stessa (vedi figura 5). Il meccanismo a flessione verticale è anche favorito dalla presenza di solai intermedi che, sotto l’effetto dell’azione sismica, esercitano sulla parete una forza inerziale orizzontale instabilizzante.
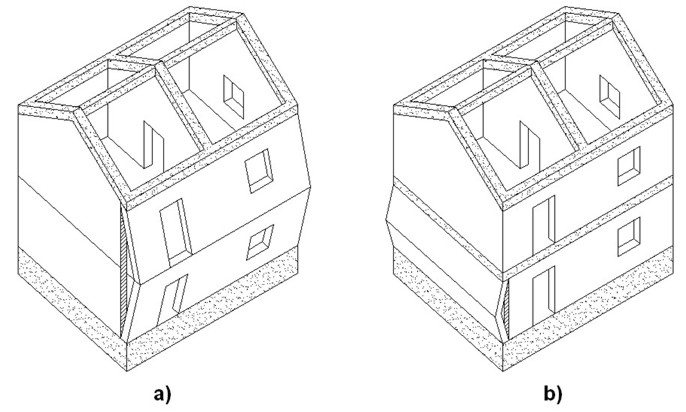
Figura 5 – Esempi di meccanismo di flessione verticale
Nel nostro esempio, la parete si considera vincolata in corrispondenza della fondazione e del tetto. Per semplicità, la cerniera cinematica si colloca in corrispondenza del solaio del primo piano f.t. (a rigore, la cerniera cinematica deve assumere la quota in corrispondenza della quale si ottiene il moltiplicatore 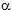 0 minore e si determina per tentativi). Lo schema del meccanismo è quello riportato in figura 6, dove si riporta la geometria dei macroelementi, le posizioni delle tre cerniere ed i carichi che gravano. Si indica con P1 il peso della parete del primo piano f.t. e con Ps1 il peso complessivo del solaio al primo piano f.t. Il valore dei carichi è riportato in tabella 4.
0 minore e si determina per tentativi). Lo schema del meccanismo è quello riportato in figura 6, dove si riporta la geometria dei macroelementi, le posizioni delle tre cerniere ed i carichi che gravano. Si indica con P1 il peso della parete del primo piano f.t. e con Ps1 il peso complessivo del solaio al primo piano f.t. Il valore dei carichi è riportato in tabella 4.

Tabella 4 – Carichi al primo piano f.t. interessati dal meccanismo
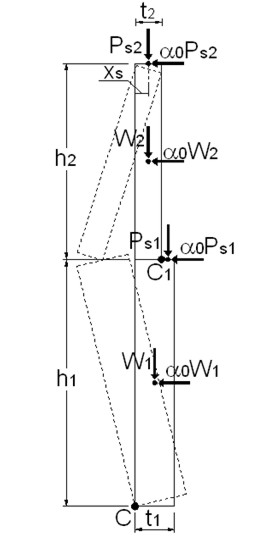
Figura 6 – Meccanismo a flessione verticale
Per non allungare notevolmente l’esempio, si riportano soltanto i risultati del meccanismo. Tenendo conto che gli elementi che partecipano al cinematismo partono dalla fondazione, occorre che sia verificata solo la (4.a). Si riportano di seguito i risultati:
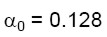 (12.a)
(12.a)
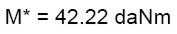 (12.b)
(12.b)
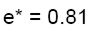 (12.c)
(12.c)
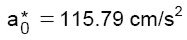 (12.d)
(12.d)
In definitiva si ottiene:
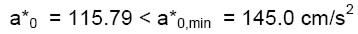 (13)
(13)
per un coefficiente di sicurezza pari a:
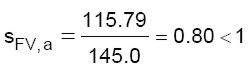 (verifica non soddisfatta) (14)
(verifica non soddisfatta) (14)
Dalla (14) si deduce che la resistenza della parete all’azione sismica (flessione verticale) è di circa l’80% di quella prevista da normativa.
Flessione orizzontale
Il meccanismo a flessione orizzontale si manifesta quando la parete in esame è ben vincolata a pareti ad essa ortogonali e non vincolata in sommità. È tipico di pareti che hanno una buona connessione con le pareti ortogonali (o trattenute da tiranti), soggette ad azioni orizzontali in testa, dovute a tetti spingenti (o forze inerziali). Anche la scarsa resistenza a trazione della muratura favorisce la formazione del meccanismo. Esempi del meccanismo descritto sono riportati in figura 7.
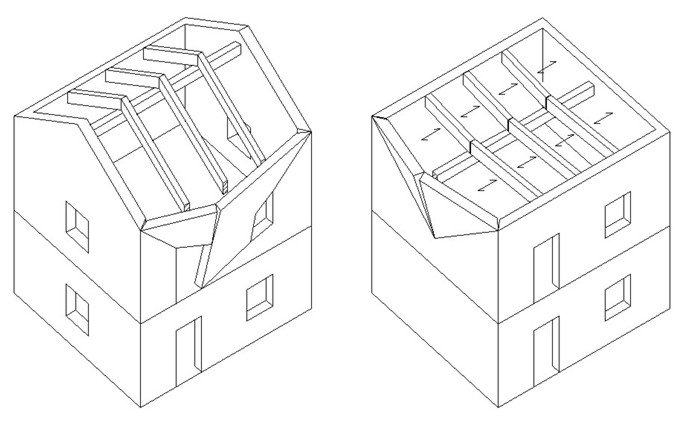
Figura 7 – Esempi di meccanismo a flessione orizzontale
Nel nostro esempio, lo schema statico può essere quello riportato in figura 8. Secondo questo modello teorico, gravano sulla parete le azioni inerziali orizzontali destabilizzanti dovute al peso dei macroelementi (P1 e P2) ed a quello delle travi del tetto (Ps2,1, Ps2,2 e Ps2,3). L’unica forza stabilizzante è la forza T (per esempio dovuta a tiranti). Per semplificare il modello, i macroelementi che partecipano al meccanismo si considerano di forma rettangolare con le cerniere verticali agli estremi (elementi tratteggiati in figura 10). A rigore, anche in questo caso la posizione della cerniera C deve essere individuata per tentativi.
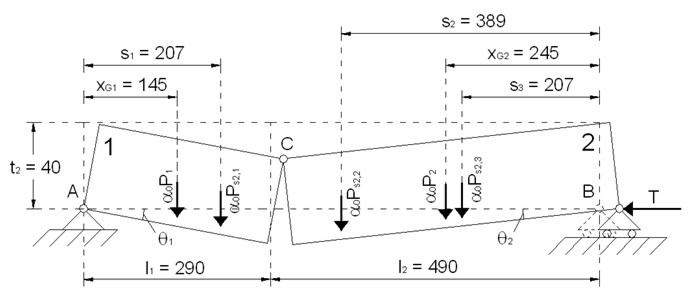
Figura 8 – Schematizzazione della parete da analizzare
Secondo questo schema, in assenza della forza T la resistenza alle azioni orizzontali è nulla (in assenza di tiranti, sotto l’effetto del sisma si hanno solo forze inerziali destabilizzanti). In definitiva si ha:
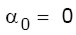 (15.a)
(15.a)
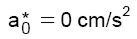 (15.b)
(15.b)
per un coefficiente di sicurezza pari a:
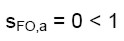 (verifica non soddisfatta) (16)
(verifica non soddisfatta) (16)
A conclusione di questa prima parte del nostro esempio (stato di fatto), si riscontra che il manufatto è molto carente dal punto di vista della resistenza alle azioni sismiche. In definitiva si ha:
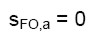 (Flessione orizzontale) (17.a)
(Flessione orizzontale) (17.a)
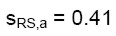 (Ribaltamento semplice) (17.b)
(Ribaltamento semplice) (17.b)
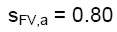 (Flessione verticale) (17.c)
(Flessione verticale) (17.c)
2. Stato di progetto (consolidamento con tiranti)
Per aumentare la resistenza sismica dell’edificio, si procede consolidando con tiranti. Come primo tentativo si collocano quattro tiranti tra loro ortogonali in corrispondenza del tetto (vedi figura 9). I tiranti collocati come sopra descritto sono influenti ai fini del meccanismo a ribaltamento semplice ed a flessione orizzontale. Non sono influenti ai fini del meccanismo a flessione verticale. Per quanto appena detto, si rielabora la struttura secondo il meccanismo di ribaltamento semplice e di flessione orizzontale.
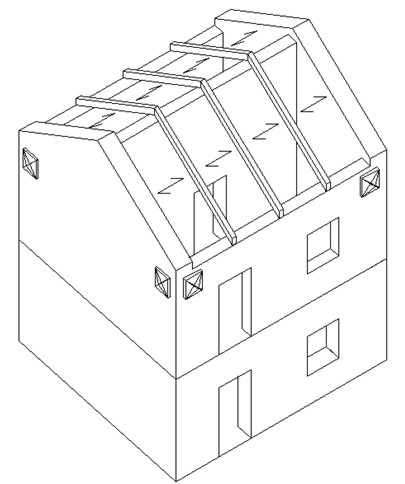
Figura 9 – Disposizione dei tiranti in corrispondenza del tetto (prima ipotesi di interventi)
Flessione orizzontale
Si progettano i tiranti partendo dal meccanismo più carente. Risolvendo il sistema riportato in figura 8, il moltiplicatore dei carichi si ottiene della seguente:
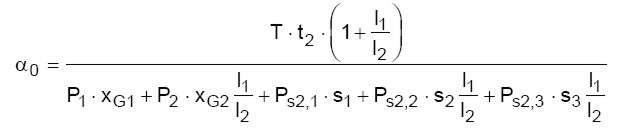 (18)
(18)
Noto il valore minimo da attribuire all’accelerazione spettrale di attivazione del meccanismo, dato dalle (4), dalla (5) si ottiene il valore minimo da attribuire al moltiplicatore dei carichi (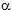 0) per l’esito positivo della verifica:
0) per l’esito positivo della verifica:
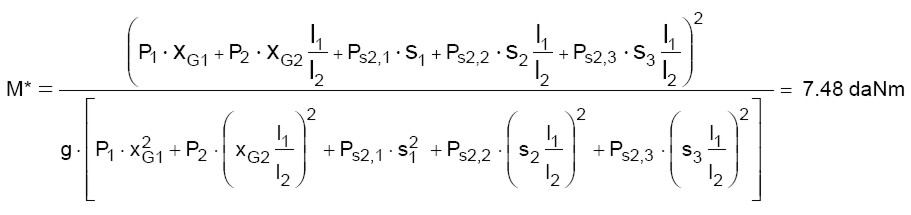 (19)
(19)
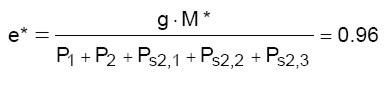 (20)
(20)
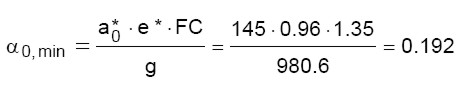 (21)
(21)
Dalla (21) si ottiene il valore minimo richiesto per il moltiplicatore dei carichi orizzontali. Dalla (18) si ottiene il valore minimo della resistenza a trazione del tirante affinché l’esito della verifica sia positivo:
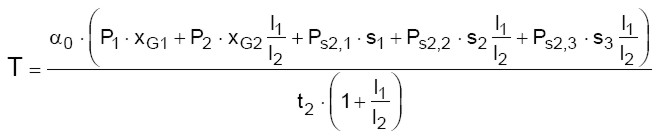 (22)
(22)
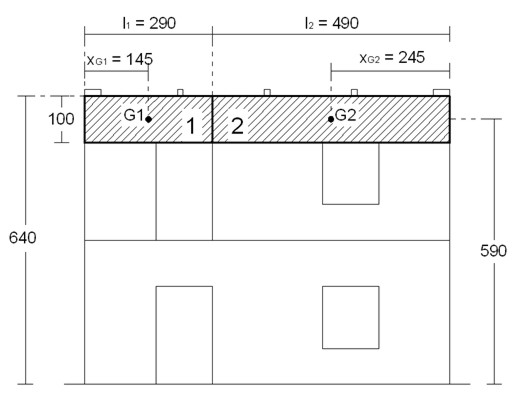
Figura10 – Dimensioni dei macroelementi

Tabella 5 – Intensità e posizione dei carichi
Sostituendo i valori numerici nella (22), tenendo conto dei carichi e delle dimensioni dei macroelementi (vedi figure 8 e 10 e tabella 5) si ottiene:
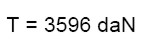 (23)
(23)
Per l’esito positivo della verifica occorre dimensionare il sistema tirante con una resistenza a trazione maggiore o uguale a 3596 daN. Si attribuiscono al tirante le dimensioni riportate in figura 11 (il tirante è stato dimensionato utilizzando il software CdT). Il tirante così dimensionato garantisce una resistenza a trazione pari a 4000 daN.
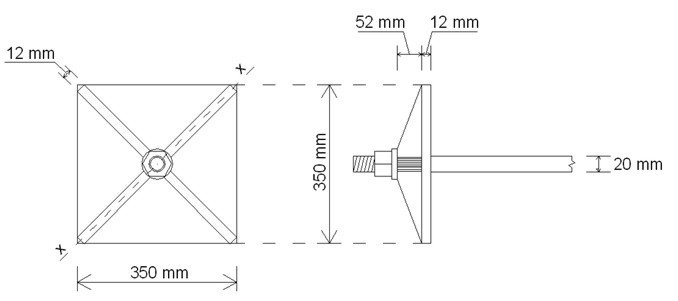
Figura 11 – Dimensioni del tirante
Effettuando la verifica tenendo conto del tirante si ottiene:
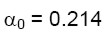 (ricavato dalla (18)) (24.a)
(ricavato dalla (18)) (24.a)
 (ricavato dalla (5)) (24.b)
(ricavato dalla (5)) (24.b)
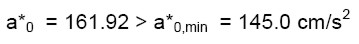 (24.c)
(24.c)
per un coefficiente di sicurezza pari a (il pedice “p” indica “post operam”):
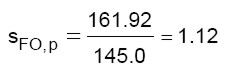 (verifica soddisfatta) (25)
(verifica soddisfatta) (25)
Ribaltamento semplice
In questo caso occorre considerare il contributo dei tiranti. Nella valutazione del moltiplicatore 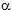 0, si aggiunge il termine stabilizzante dovuto ai tiranti (vedi figura 12).
0, si aggiunge il termine stabilizzante dovuto ai tiranti (vedi figura 12).
Dall’equilibrio alla rotazione intorno alla cerniera cinematica C si ottiene il seguente valore del moltiplicatore di attivazione del meccanismo:
 (26)
(26)
In definitiva si ottiene:
 (27)
(27)
per un coefficiente di sicurezza pari a:
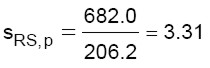 (verifica soddisfatta) (28)
(verifica soddisfatta) (28)
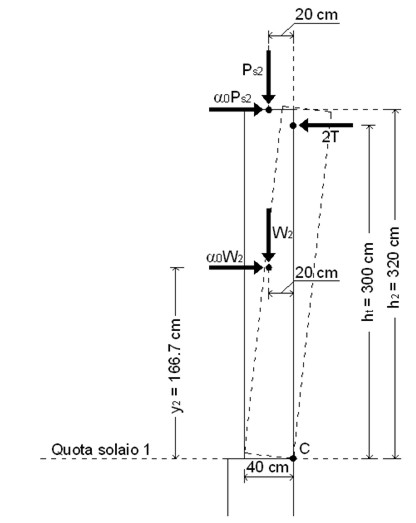
Figura 12 – Posizione dei carichi
Pressoflessione verticale
La disposizione dei tiranti in corrispondenza del tetto consentono di migliorare l’esito della verifica per il ribaltamento semplice e la flessione orizzontale. Non forniscono alcun miglioramento al meccanismo a flessione verticale. Con questa disposizione dei tiranti, risultano verificati il meccanismo a ribaltamento semplice (sRS,p = 3.31) e quello a flessione orizzontale (sFO,p = 1.12). Il meccanismo a flessione verticale continua a non verificare (sFV,a = 0.80). Se ci si accontenta di questi risultati, anche se la struttura non è del tutto adeguata, si ottiene un risultato lo stesso importante in quanto il coefficiente di sicurezza passa da 0 a 0.8. Se si vuole migliorare ulteriormente il comportamento della struttura occorre procedere con ulteriori interventi. Per aumentare la resistenza della struttura occorre collocare i tiranti anche in corrispondenza del solaio al primo piano f.t. (vedi figura 13).
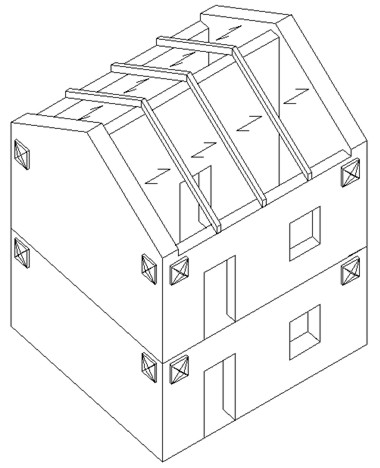
Figura 13 – Disposizione dei tiranti in corrispondenza del solaio al primo piano f.t. (seconda ipotesi di interventi)
I tiranti collocati in corrispondenza del solaio del primo impalcato hanno funzione stabilizzante in quanto si oppongono alla rotazione dei macroelementi con una forza pari alla loro resistenza (vedi schema riportato in figura 14). Per poter ruotare, i macroelementi devono vincere la forza 2∙T.
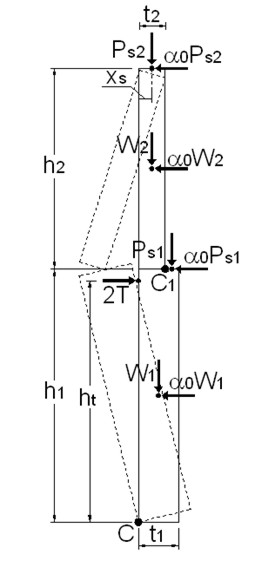
Figura 14 – Meccanismo a flessione verticale
Si riportano di seguito i risultati:
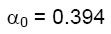 (29.a)
(29.a)
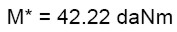 (29.b)
(29.b)
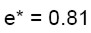 (29.c)
(29.c)
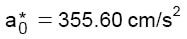 (29.d)
(29.d)
In definitiva si ottiene:
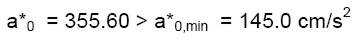 (30)
(30)
per un coefficiente di sicurezza pari a:
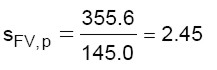 (verifica soddisfatta) (31)
(verifica soddisfatta) (31)
3. Conclusioni
L’obiettivo di questo semplicissimo esempio è quello di mettere in evidenza l’efficacia di un consolidamento con tiranti su un edificio in muratura. Si è partiti da un edificio con resistenza sismica nulla, sono stati applicati tiranti in corrispondenza del solaio al primo impalcato e del tetto, ottenendo un edificio adeguato alle esigenze di normativa (solo per quanto riguarda l’analisi dei meccanismi locali). Naturalmente, l’esempio è stato svolto con criteri semplificati, senza tenere conto di molti fenomeni che si possono verificare nella realtà (un esempio tra tutti può essere la resistenza illimitata dei macroelementi). Probabilmente, a seguito di un evento sismico, anche le strutture consolidate con tiranti possono subire danni ed anche crolli, ma ciò che si può affermare con certezza è che gli edifici consolidati hanno molte più possibilità di resistere agli eventi. Rimane inoltre da sottolineare che l’intervento per come riportato nell’esempio, non richiede enormi sforzi economici.
Bibliografia
 [1] Michele Vinci - I tiranti in acciaio nel calcolo delle costruzioni in muratura – Dario Flaccovio Editore – 2014
[1] Michele Vinci - I tiranti in acciaio nel calcolo delle costruzioni in muratura – Dario Flaccovio Editore – 2014
 [2] Michele Vinci - Metodi di calcolo e tecniche di consolidamento per edifici in muratura – III edizione – 2019
[2] Michele Vinci - Metodi di calcolo e tecniche di consolidamento per edifici in muratura – III edizione – 2019
 I tiranti in acciaio nel calcolo delle costruzioni in muratura
I tiranti in acciaio nel calcolo delle costruzioni in muratura
Software utilizzati
 Software CdT (Calcolo di tiranti)
Software CdT (Calcolo di tiranti)
 Software STR (Spettri e Tempi di Ritorno)
Software STR (Spettri e Tempi di Ritorno)
 Software EsT (Esempi tratti dal testo)
Software EsT (Esempi tratti dal testo)