Gli FRP come alternativa per il consolidamento degli edifici in muratura
(comportamento nel piano)
 Articolo disponibile anche in formato PDF
Articolo disponibile anche in formato PDF
 Metodi di calcolo e tecniche di consolidamento per edifici in muratura - III edizione - 2019
Metodi di calcolo e tecniche di consolidamento per edifici in muratura - III edizione - 2019
Gli FRP rappresentano una valida alternativa per il consolidamento di elementi in muratura. Possono essere utilizzati sia per aumentare la resistenza nel piano che fuori piano di una parete. In questo contesto si vuole mettere in risalto come l’utilizzo del rinforzo modifica il comportamento nel piano della parete, rendendola più resistente.
Gli FRP contribuiscono sia per incrementare la resistenza a pressoflessione che a taglio di maschi murari e di fasce di piano.
Il comportamento di un elemento in muratura consolidato con materiali compositi è simile a quello di un elemento in calcestruzzo. Il rinforzo verticale (nel caso di un maschio murario) ha la stessa funzione dell’armatura longitudinale, quello orizzontale ha la stessa funzione delle staffe e la muratura ha la stessa funzione del calcestruzzo (vedi figura 1).
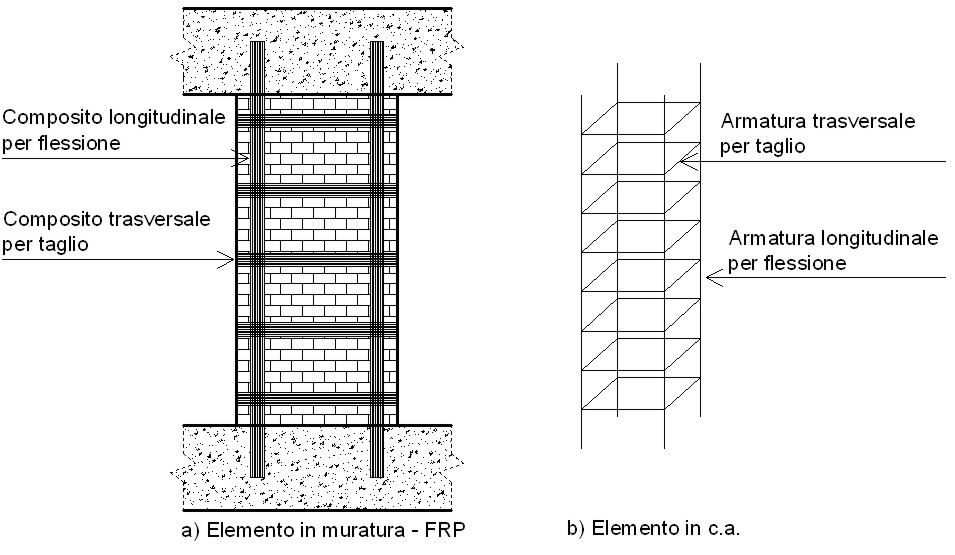
Figura 1
Ai fini della verifica a pressoflessione, a differenza della teoria sugli elementi in calcestruzzo, cambiano i legami costitutivi che definiscono i materiali. Il legame costitutivo che definisce la muratura è elastico – perfettamente plastico, mentre quello che definisce il composito è elastico lineare fino a rottura (vedi figura 2). Per la verifica agli Stati Limite Ultimi (SLU), si fanno le seguenti ipotesi:
- Mantenimento delle sezioni piane;
- Perfetta aderenza tra muratura e materiale composito;
- Resistenza nulla a trazione per la muratura;
- Resistenza nulla a compressione per il composito;
- Comportamento elastico-perfettamente plastico per la muratura;
- Comportamento elastico lineare fino a rottura per il composito.
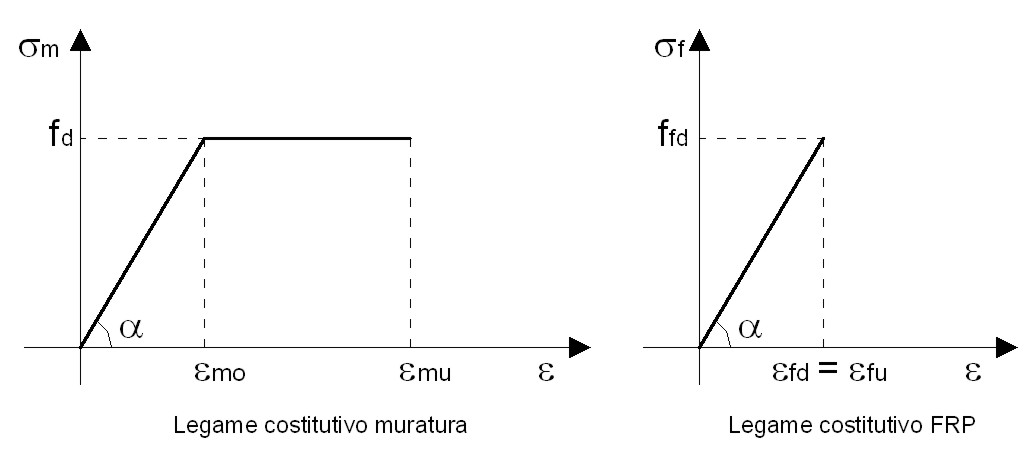
Figura 2
Per i legami definiti in figura 2, dalla teoria agli stati limite si ottengono 6 campi di rottura per come riportato in figura 3 (per una trattazione completa sulle grandezze che definiscono i campi di rottura si rimanda al testo riportato in bibliografia).
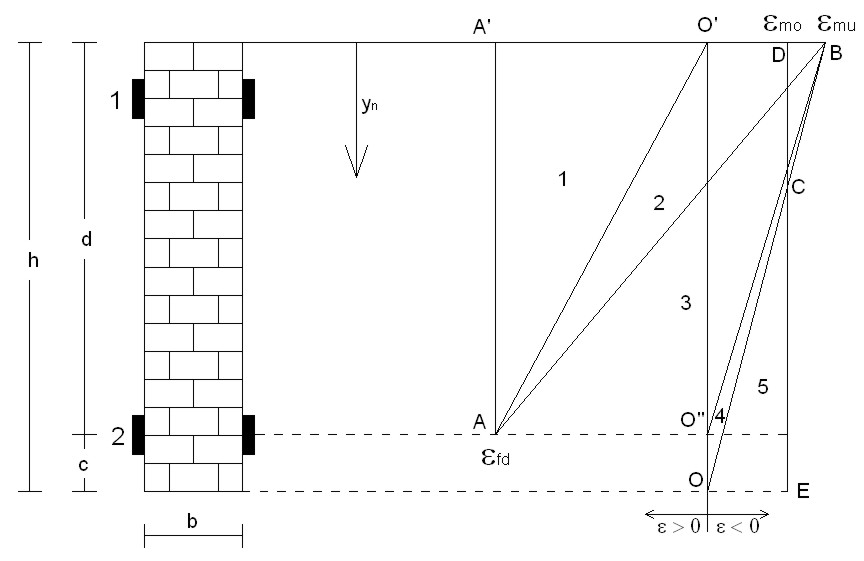
Figura 3
Il dominio di resistenza a pressoflessione di un elemento consolidato con FRP è simile a quello (in grassetto) riportato in figura 4. In corrispondenza degli sforzi normali massimi il dominio dell’elemento consolidato è pressoché coincidente con quello non consolidato. Ciò è dovuto all’ipotesi di resistenza a compressione nulla degli FRP (per sezioni molto compresse il consolidamento da contributo trascurabile). Nel caso della pressoflessione, il consolidamento è inefficace per elementi molto compressi e molto efficace per elementi poco compressi. Inoltre, a differenza degli elementi in muratura non consolidati, quelli consolidati consentono anche sollecitazioni assiali di trazione. Per alcuni valori di trazione dello sforzo normale (ascisse negative in figura), il momento resistente è diverso da zero, circostanza non possibile per elementi in muratura non consolidati. Sempre ai fini della pressoflessione, gli FRP sono indicati per consolidare elementi in muratura ai piani alti di una costruzione (poco compressi) e poco indicati per consolidare elementi ai piani bassi (molto compressi). Naturalmente, i concetti appena esposti sono validi per edifici costituiti da molti piani. Generalmente, per edifici con pochi piani, gli sforzi normali sono sempre tali da far apprezzare incrementi di resistenza a pressoflessione anche per gli elementi ai piani bassi.
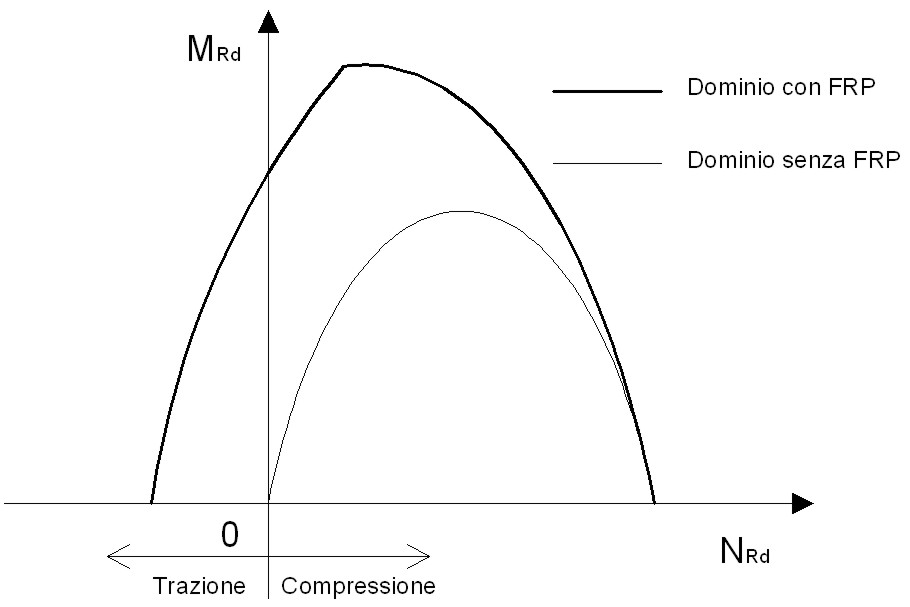
Figura 4
Per la verifica a taglio si adotta la stessa teoria utilizzata nel cemento armato del traliccio isostatico di Ritter-Morsch (vedi figura 5). La resistenza di progetto a taglio della muratura rinforzata (VRd) è calcolata come somma della resistenza della muratura (VRd,m) e quella del rinforzo (VRd,f). In formule si ha:
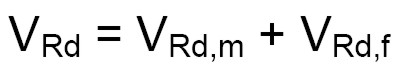 (1)
(1)
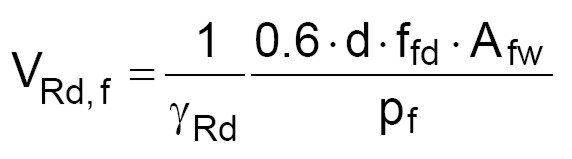 (2.a)
(2.a)
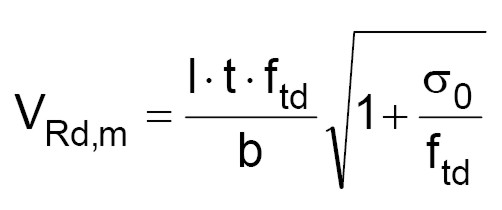 (2.b)
(2.b)
dove
- ffd è la resistenza di calcolo del composito;
- Afw è l’area di ogni singolo rinforzo a taglio disposta in direzione parallela alla forza di taglio;
- pf è il passo degli elementi di rinforzo paralleli alla forza di taglio.
- ftd è la resistenza di calcolo a trazione della muratura;
- l è la lunghezza della sezione trasversale dell’elemento;
- t è lo spessore dell’elemento:
- b è il coefficiente che tiene conto della snellezza del maschio.
Dalla (2.a) si intuisce che la resistenza a taglio aumenta all’aumentare dell’area Afw ed al diminuire del passo pf.
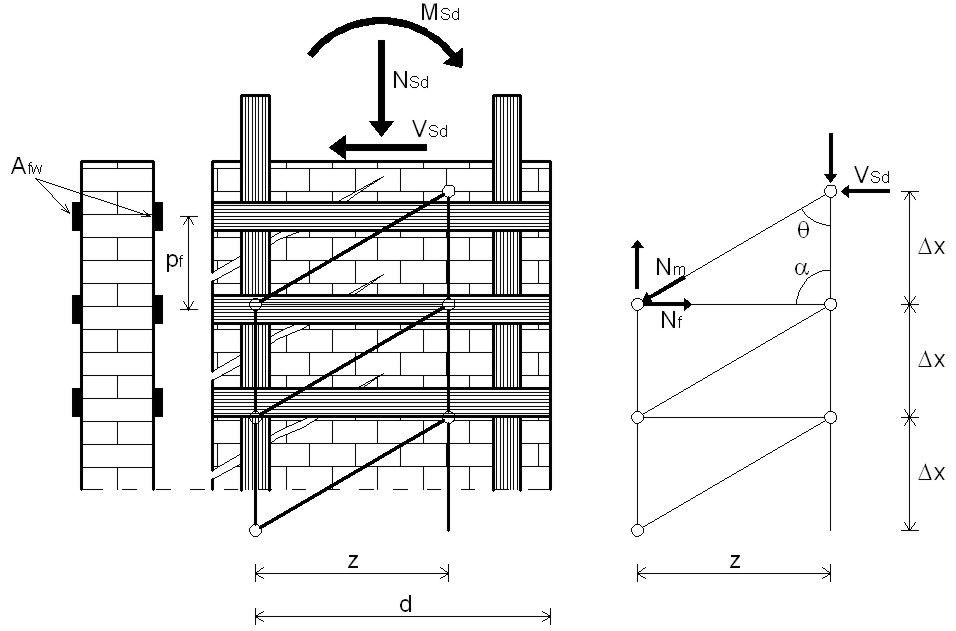
Figura 5
Esempio
Data la parete riportata in figura 6, consolidare con FRP in modo da soddisfare le verifiche a pressoflessione e taglio.
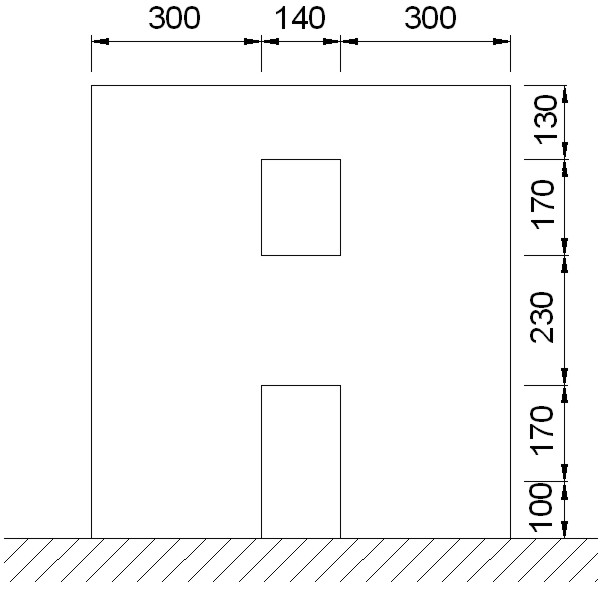
Figura 6
Dati
- Spessore della parete: 40 cm
- Materiale: mattoni pieni e malta di calce
- Peso complessivo del solaio: 750 daN/m2
- Sviluppo solaio (su ogni lato della parete): 3 m
- Livello di conoscenza: LC1
- Coefficiente di sicurezza della muratura (
 m): 2
m): 2
Risultati
Per mettere in evidenza le potenzialità del consolidamento con FRP, semplifichiamo l’esempio ipotizzando la parete sottoposta alla sola azione sismica (l’obiettivo è quello di evidenziare come il consolidamento altera il comportamento della parete). La parete viene risolta secondo l’analisi statica equivalente.
Nella prima fase si risolve la parete senza interventi. Per la schematizzazione si adotta la tecnica del telaio equivalente, secondo la quale si considera costituita da fasce di piano, maschi murari e conci rigidi (vedi figura 7). Poiché non sono presenti elementi resistenti a trazione nelle fasce di piano (tiranti, cordoli, FRP, ecc.), queste ultime possono essere considerate nel modello solo come elementi di collegamento, senza poter trasmettere sollecitazioni di flessione e taglio. Le fasce di piano vengono considerate incernierate agli estremi (vedi figura 8).
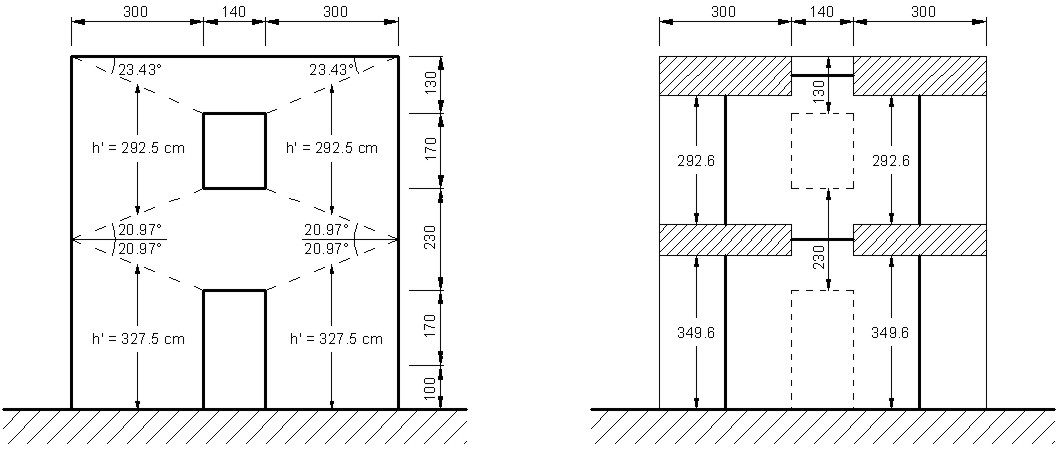
Figura 7
Per semplicità si effettua la verifica di un solo maschio murario (appartenente al primo piano fuori terra) e di una sola fascia di piano (compresa tra le due aperture della parete).
I parametri di calcolo della muratura (mattoni pieni e malta di calce), vengono riassunti nella tabella 1 (vedi punto C8.A.2 della Circolare 617/2009). Poiché si è ipotizzato il livello di conoscenza LC1, per le resistenze si parte dai valori minimi riportati nella tabella C8A.2.1 della Circolare 617/2009 e si dividono per il fattore di confidenza (FC = 1.35) ed il coefficiente di sicurezza ( m = 2). Per i moduli elastici si assumono i valori medi riportati sempre nella tabella della Circolare.
m = 2). Per i moduli elastici si assumono i valori medi riportati sempre nella tabella della Circolare.

Tabella 1 – Caratteristiche meccaniche della muratura
Per ipotesi, sul modello agisce solo la forza sismica valutata attraverso la tecnica dell’analisi statica equivalente. La forza sismica si considera applicata a quota dei due solai (la forza totale di ogni piano viene divisa equamente ai due conci rigidi). Per evitare di allungare inutilmente il documento, si dà per scontata l'entità delle forze sismiche e si prendono per buone le sollecitazioni riportate nei diagrammi e nelle tabelle (lo scopo dell’esempio è quello di vedere il comportamento della parete consolidata con FRP e non quello di determinare le sollecitazioni sugli elementi).
Applicando l’analisi statica equivalente sul modello (schema statico di figura 8), si ottengono le sollecitazioni riportate in tabella 2 (al piede per il maschio ed agli estremi per la fascia). Lo sforzo normale è nullo per l’ipotesi di considerare solo l’azione sismica orizzontale e per il vincolo cerniera agli estremi delle fasce di piano. Il comportamento della parete è simile a quello di una mensola. In figura 8 si riporta anche il diagramma dei momenti.
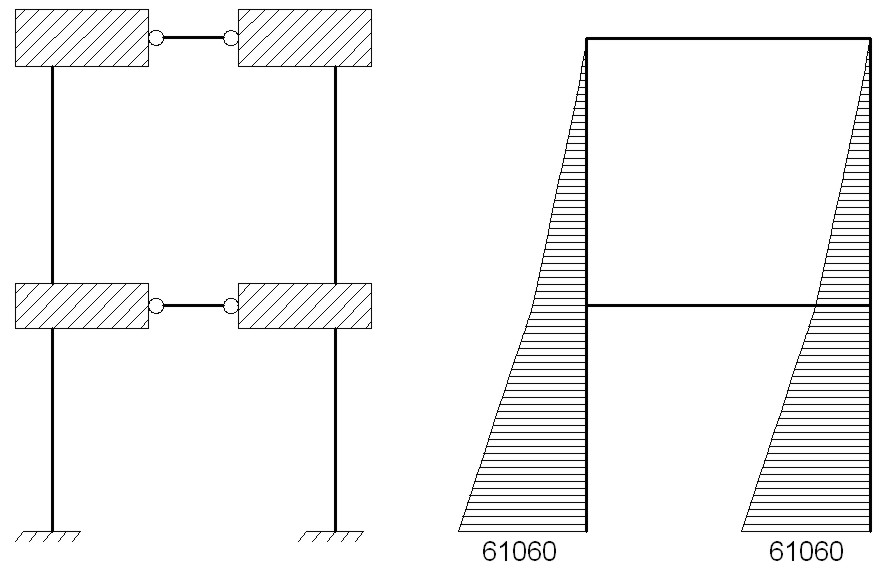
Figura 8 – Schema statico e diagramma dei momenti

Tabella 2 – Sollecitazioni per modello con fasce di piano incernierate agli estremi
Per lo schema statico adottato, occorre effettuare le verifiche a pressoflessione e taglio soltanto del maschio murario (in questa fase le fasce di piano non devono essere verificate in quanto incernierate agli estremi). Poiché lo sforzo normale è nullo ( 0 = 0), sarà nullo anche il momento resistente:
0 = 0), sarà nullo anche il momento resistente:
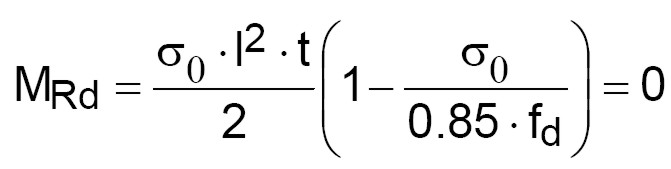 (3)
(3)
Nella figura 9 si riporta il dominio di resistenza del maschio murario non consolidato ed il punto rappresentativo dello stato sollecitazionale. Come si vede dalla stessa figura, la verifica a pressoflessione non è soddisfatta.
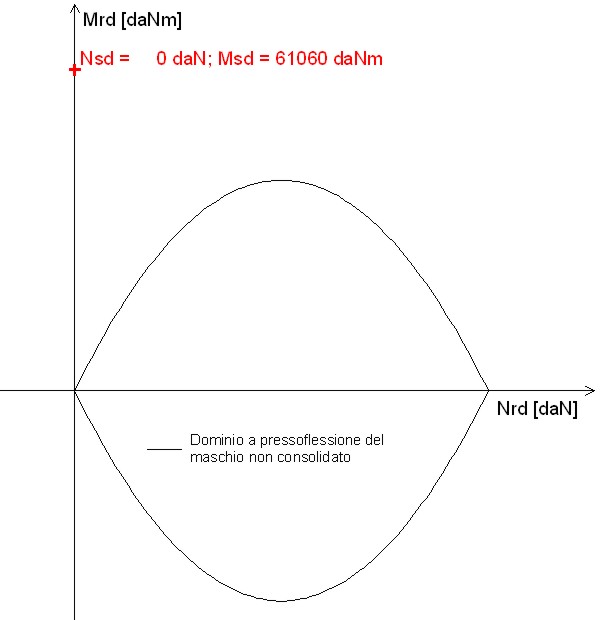
Figura 9 – Dominio di resistenza per il maschio murario (maschio senza interventi)
Il taglio resistente del maschio murario senza interventi si ottiene dalla (2.b):
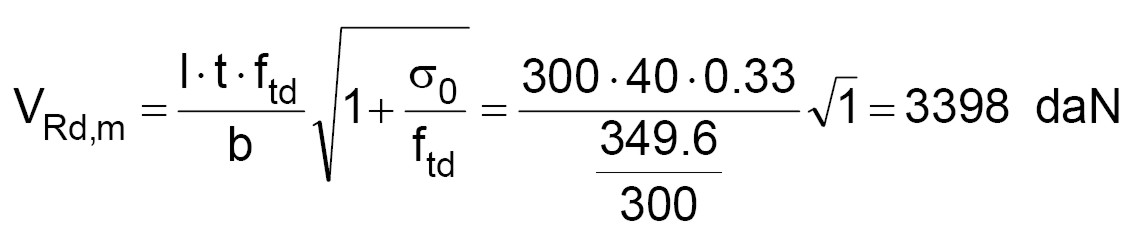 (4)
(4)
minore del taglio sollecitante (VSd) riportato in tabella 2.
Per migliorare le condizioni della parete si procede con il consolidamento della stessa attraverso l’utilizzo di FRP, le cui caratteristiche sono riportate in tabella 3 (per approfondire su come si ricavano i dati geometrici ed i parametri meccanici che definiscono il rinforzo consultare il testo citato in bibliografia). Si indica con b la larghezza, con t lo spessore, con Ef il modulo elastico, con  fd la deformabilità limite e con ffd la resistenza di calcolo del composito.
fd la deformabilità limite e con ffd la resistenza di calcolo del composito.

Tabella 3 – Parametri meccanici e geometrici per gli FRP
Come prima ipotesi di intervento si consolidano le fasce di piano con due strisce orizzontali per ogni piano e su ogni lato della parete (vedi “a” di figura 10).
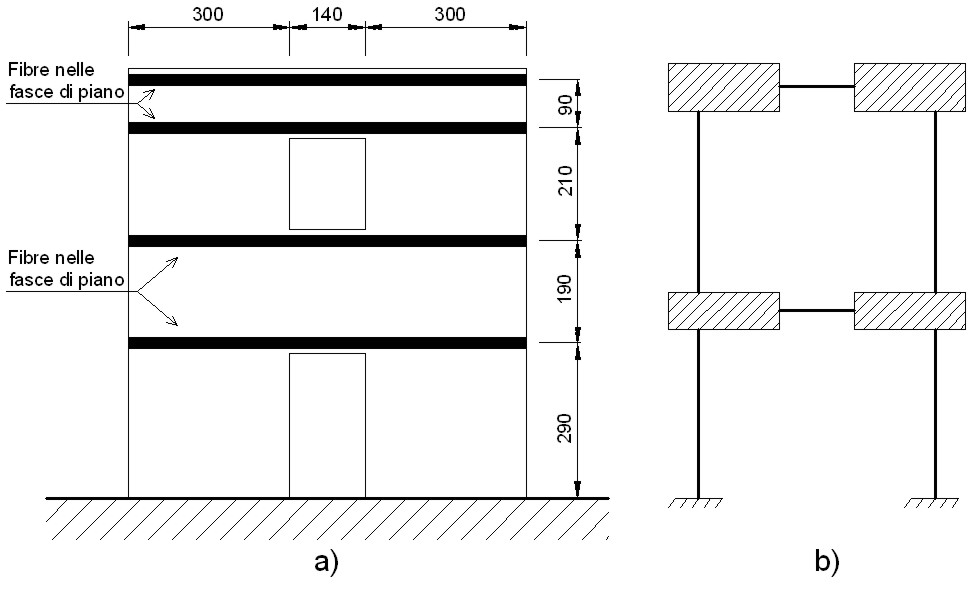
Figura 10 – a) Collocazione FRP (prima ipotesi di intervento); b) Schema statico
La presenza degli FRP nelle fasce di piano consente di modificare lo schema statico della struttura. Poiché costituiscono un elemento resistente a trazione nelle fasce di piano, queste ultime possono trasmettere flessione e taglio agli elementi a cui sono collegati (vengono incastrate ai conci rigidi adiacenti – vedi “b” di figura 10). Questo cambiamento comporta una variazione notevole delle sollecitazioni che vengono riassunte nella tabella 4. Il comportamento della parete non è più a mensola ma a telaio.

Tabella 4 – Sollecitazioni per modello con fasce di piano incastrate agli estremi
Per effetto della presenza del consolidamento nelle fasce di piano, lo sforzo normale nei maschi murari è diverso da 0, per cui si ha:
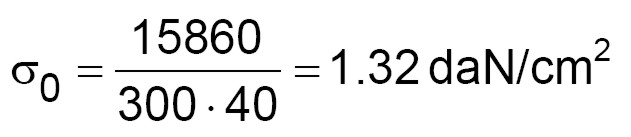 daN/cm2 (5)
daN/cm2 (5)
La resistenza a pressoflessione vale:
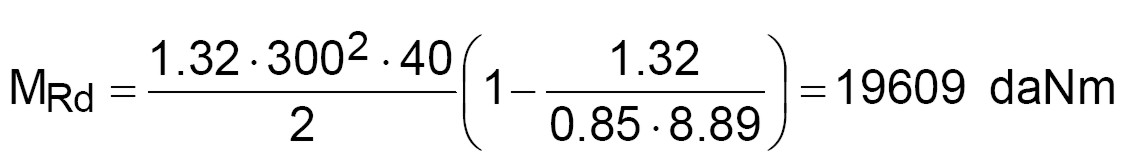 (6)
(6)
Nella figura 11 si riporta il dominio di resistenza del maschio murario ed il punto rappresentativo dello stato sollecitazionale a seguito del consolidamento delle fasce di piano (il dominio si riferisce al maschio murario non consolidato con FRP - l'intervento è stato applicato alle sole fasce). La verifica a pressoflessione non è ancora soddisfatta, ma le condizioni sono migliori rispetto al caso con fasce di piano non consolidate. Da notare come il consolidamento delle fasce di piano comporta un miglioramento delle condizioni anche per i maschi murari. Per il maschio murario si verificano due effetti positivi: la riduzione del momento sollecitante (si passa da 61060 daNm a 26167 daNm) e l’aumento dello sforzo normale sollecitante (si passa da 0 daN a 15860 daN).
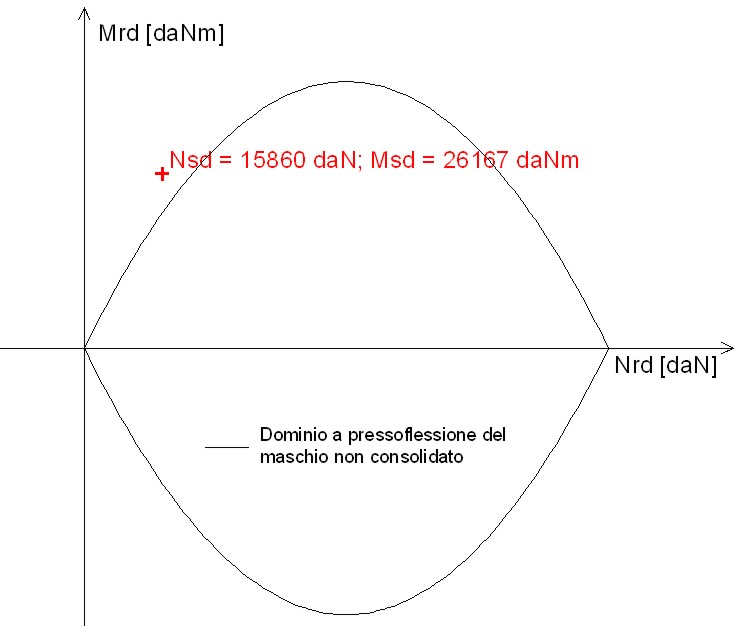
Figura 11 – Dominio di resistenza per il maschio murario (caso con FRP nelle fasce di piano)
Per quanto riguarda la verifica a taglio, per la particolare geometria della struttura, il taglio sollecitante rimane immutato, mentre, per via del diverso valore dello sforzo normale ( 0 ≠ 0), varia il taglio resistente:
0 ≠ 0), varia il taglio resistente:
 (7)
(7)
Poiché il taglio sollecitante è VSd = 10131 daN, ne consegue che l’esito della verifica è ancora negativo. Occorre incrementare il taglio resistente in modo da essere maggiore o uguale a quello sollecitante (VRd ≥ VSd).
Per l’esito negativo delle verifiche (sia a pressoflessione e a taglio), si procede consolidando con FRP anche i maschi murari. Si adotta lo stesso materiale utilizzato per le fasce di piano. Nella figura 12 si riporta la disposizione delle fibre.
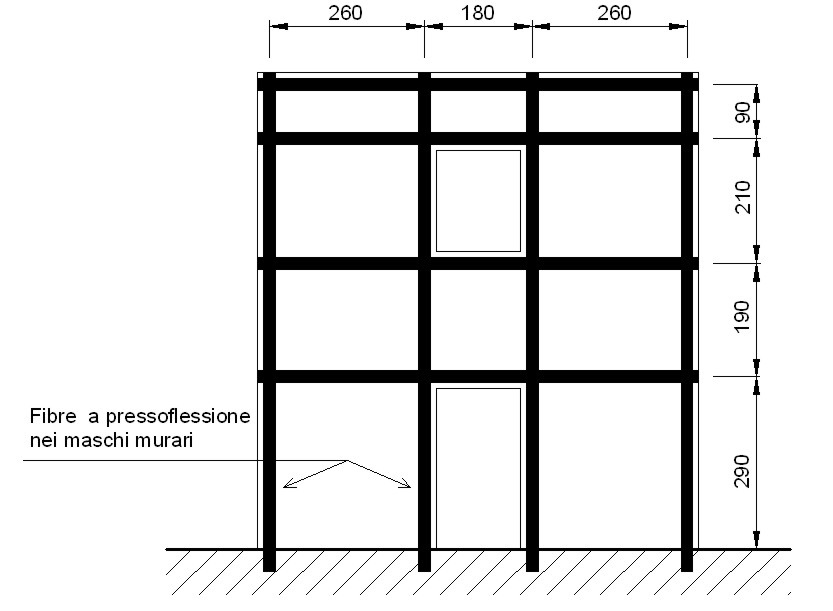
Figura 12 – Disposizione delle fasce in FRP (seconda ipotesi di intervento)
Gli elementi verticali collocati nei maschi murari hanno il compito di incrementarne la resistenza a pressoflessione. Per il valore dello sforzo normale sollecitante si ottiene la soluzione della sezione riportata in figura 13.
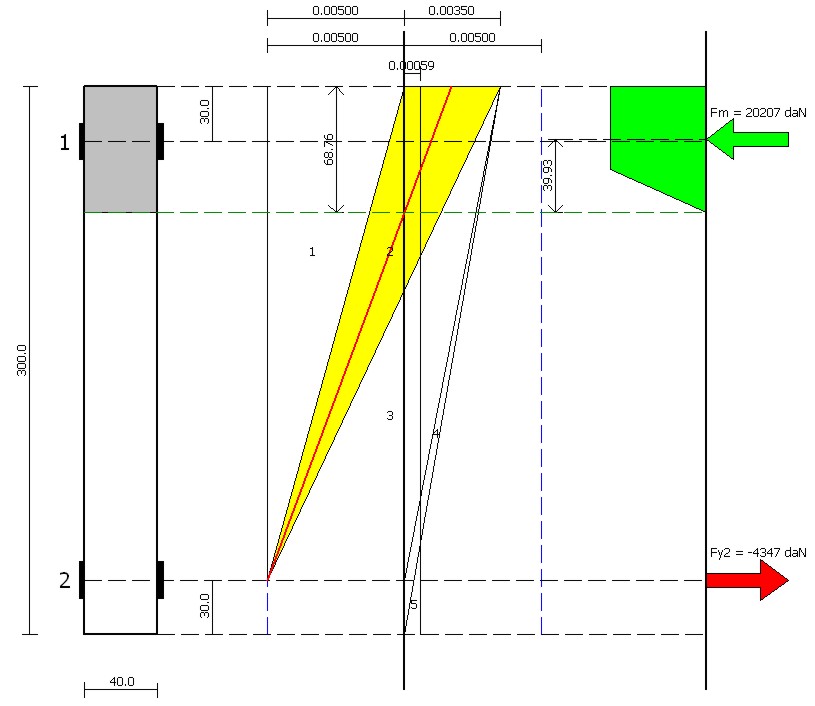
Figura 13 – Soluzione della sezione
Il campo di rottura (evidenziato in giallo) è il 2 e l’asse neutro si trova ad una distanza di 68.76 cm dal lembo compresso. Alle sollecitazioni esterne si oppongono la resistenza a compressione della muratura pari a 20207 daN (forza verde in figura) e la forza di trazione del composito pari a 4347 daN (forza rossa in figura). Il composito in compressione (denominato con “1” in figura) non da alcun contributo alla resistenza della sezione. Dall’equilibrio alla rotazione intorno all’asse baricentrico della sezione si ottiene (i valori delle forze e le distanze dall’asse baricentrico si possono ricavare dalla figura 13):
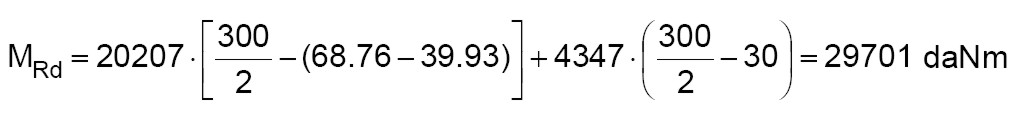
Nella figura 14 si riporta tutto il dominio della sezione. Il dominio in grassetto è quello della muratura consolidata. Per valori bassi dello sforzo normale si apprezzano incrementi del momento resistente, mentre, per valori alti il dominio coincide con quello della sezione non consolidata (quest’ultimo rappresentato dalla curva sottile in figura). In corrispondenza dello sforzo normale sollecitante (NSd = 15860 daN), il momento resistente (NRd = 29701 daNm) aumenta sufficientemente per l’esito positivo della verifica (stato sollecitazionale interno del dominio di resistenza).
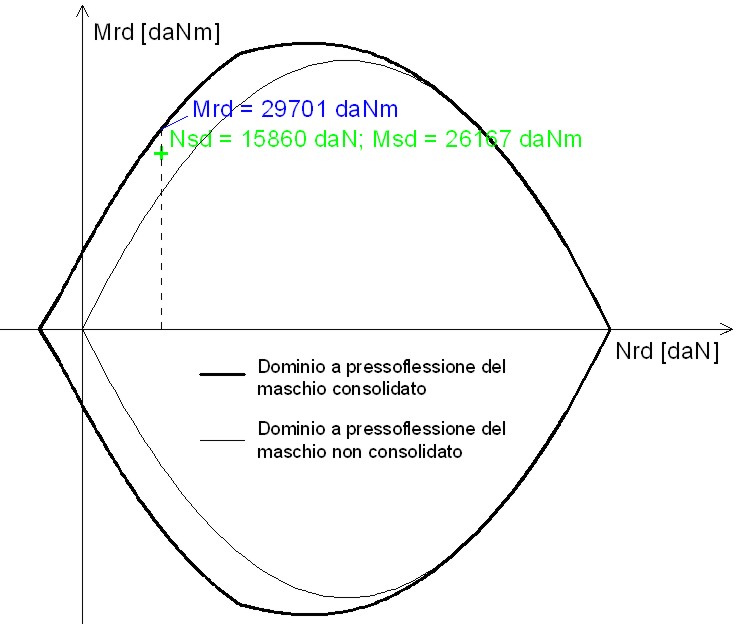
Figura 14 – Dominio di resistenza per il maschio murario consolidato con FRP
In quest’ultimo caso, il punto rappresentativo dello stato sollecitazionale è interno al dominio di resistenza a pressoflessione della sezione. A questo punto, per il maschio murario la verifica a pressoflessione è soddisfatta. Poiché il valore dello sforzo normale sollecitante è relativamente basso, il consolidamento risulta essere efficace.
Gli FRP possono essere utilizzati anche per incrementare la resistenza a taglio di una parete. Su ogni maschio murario del primo piano si collocano tre fasce orizzontali (vedi figura 15), due agli estremi del maschio ed uno in mezzeria (tre fasce sono necessarie per garantire la formazione del traliccio isostatico).
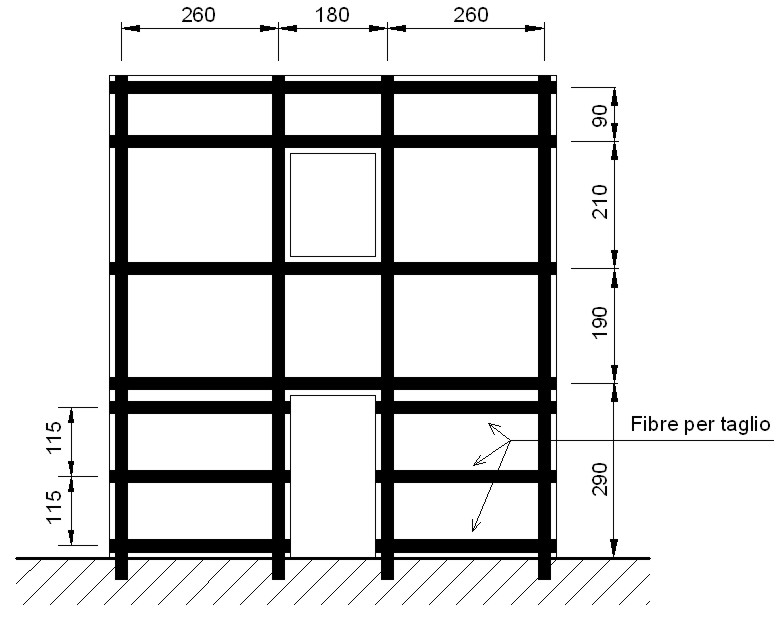
Figura 15 – Disposizione delle fasce in FRP (terza ipotesi di intervento)
Dalla (2.a) si ottiene:
 (8)
(8)
Sommando i contributi della (7) e della (8) si ottiene:
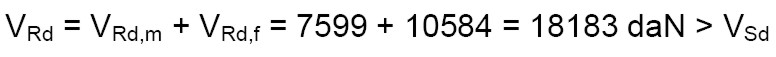 (9)
(9)
Anche per il taglio la verifica è soddisfatta.
Rimane da verificare la fascia di piano (occorre verificare anche le fasce di piano in quanto incastrate agli estremi). Le verifiche sono analoghe a quelle per il maschio murario. Poiché lo sforzo normale è nullo, in assenza di FRP, la verifica a pressoflessione è negativa. Il consolidamento consente di ottenere un momento resistente maggiore di zero anche in corrispondenza dello sforzo normale nullo (vedi figura 16). Dalla figura si evince che l’esito della verifica è positivo (punto rappresentativo delle sollecitazioni interno al dominio di resistenza).
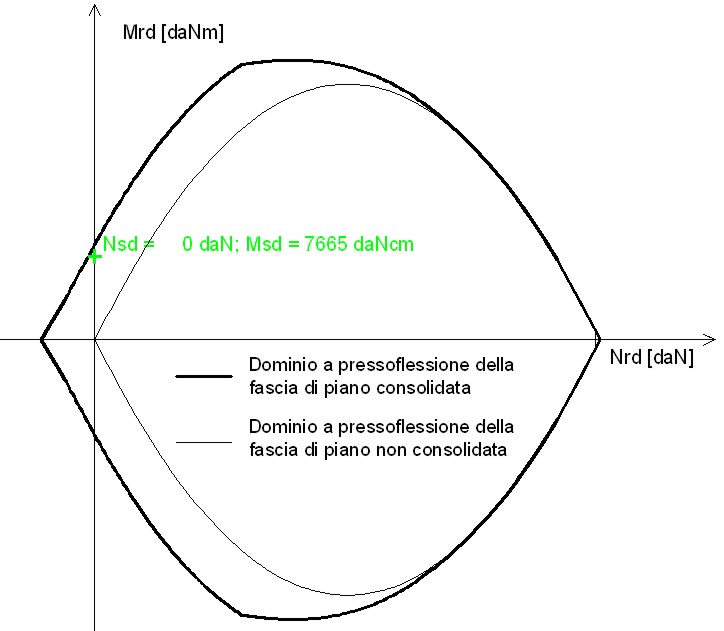
Figura 16 – Dominio di resistenza per la fascia di piano consolidata con FRP
Per la verifica a taglio, il taglio resistente della sola muratura è dato dalla seguente:
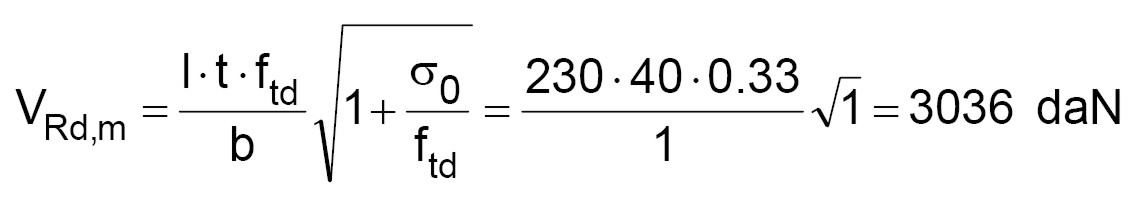 (10)
(10)
minore di quello sollecitante pari a 10951 daN (vedi tabella 4). Per incrementare la resistenza si consolida la fascia di piano con elementi ortogonali all’asse della stessa fascia (elementi in FRP verticali all’interno della fascia di piano – vedi figura 17).
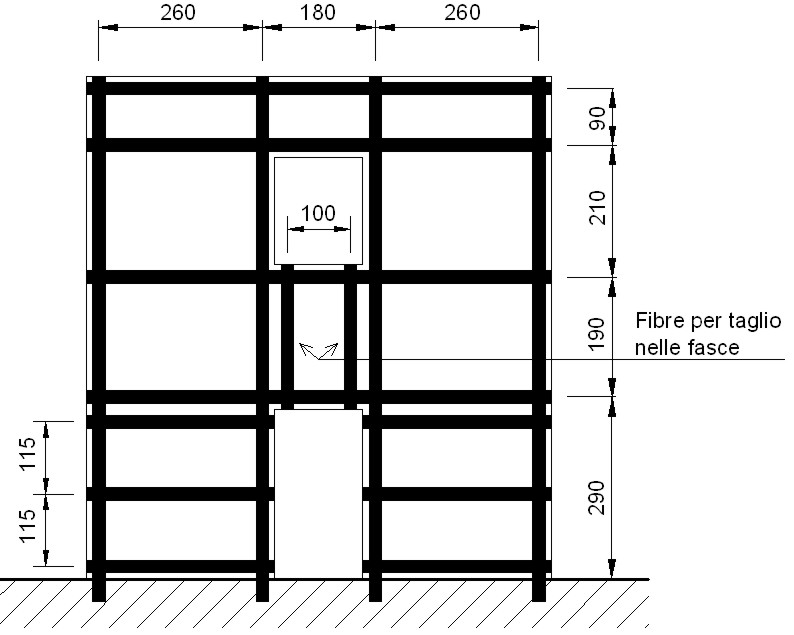
Figura 17 – Disposizione degli FRP nella fascia di piano (quarta ipotesi di interventi)
Il contributo fornito dalla presenza degli FRP si ricava dalla (2.a):
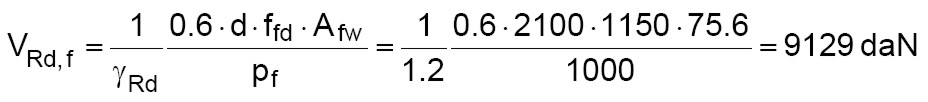 (11)
(11)
Sommando i contributi della (10) e della (11) si ottiene:
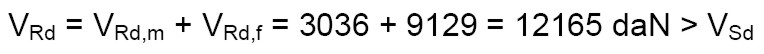 (12)
(12)
Anche per il taglio la verifica è soddisfatta.
Osservazione
Le considerazioni fatte sono valide per il maschio murario compresso. Ovviamente, a seguito del consolidamento delle fasce di piano, per la simmetria della struttura, un maschio murario si comprime mentre l’altro si decomprime dello stesso valore di sforzo normale con conseguente esito negativo della verifica. Naturalmente, in un contesto reale occorre combinare l’azione sismica con i carichi gravitazionali che vanno a ridurre l’azione assiale di trazione (generalmente, sotto l’effetto di tutti i carichi, i maschi murari sono compressi anche sotto l’effetto di azioni sismiche rilevanti).
Bibliografia
 Michele Vinci - Metodi di calcolo e tecniche di consolidamento per edifici in muratura – Dario Flaccovio Editore – 2012
Michele Vinci - Metodi di calcolo e tecniche di consolidamento per edifici in muratura – Dario Flaccovio Editore – 2012
Software utilizzato
FRP – scaricabile gratuitamente dal sito www.edificiinmuratura.it