Lo scopo del documento è quello di mettere in evidenza l’importanza dei collegamenti tra orizzontamenti ed elementi in muratura e come incidono sulla resistenza delle pareti. In questo contesto si discute solo di carichi verticali, tralasciando gli effetti dovuti ad azioni sismiche (o di altra natura). Quanto detto viene documentato attraverso un esempio di verifica. Infine si riporta un possibile particolare costruttivo pensato per ridurre gli effetti dell’eccentricità dei carichi sulle pareti e quindi per aumentarne la resistenza.

Scarica articolo in formato pdf

Scarica particolari costruttivi in formato dwg

1 – Introduzione

Come si sa, la muratura è un materiale non resistente a trazione. Questo comporta, di conseguenza, che se un carico è eccentrico rispetto all’asse della parete, la parete stessa tende a parzializzarsi (retta di azione del carico verticale fuori dal terzo medio della sezione trasversale della parete – vedi figura 1).

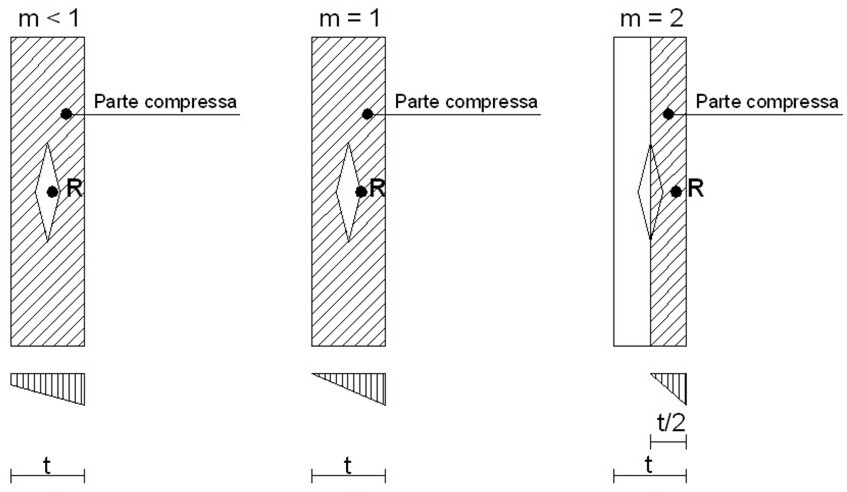
Figura 1 – Stato della sezione per diverse posizioni della retta di azione della forza verticale

Naturalmente la parzializzazione in una parete ne riduce la resistenza, quindi se l’appoggio causa parzializzazioni, si capisce il ruolo importante che ricopre, soprattutto in fase di progettazione. Un elemento di un solaio semplicemente appoggiato su una parete genera sicuramente un’eccentricità. Le suddette eccentricità possono essere limitate se tra elemento di solaio e muratura si realizzano appositi dispositivi.

2 – Verifica della parete

Per dimostrare quanto sopra detto si effettua sulla parete su cui grava il carico (solaio, capriata, ecc.) la verifica a pressoflessione per carichi laterali, riportata nel punto 4.5.6.2 del D.M. 14/01/2008. Tale verifica si ritiene soddisfatta se è verificata la seguente condizione:

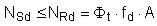                                                                              (1)

dove

• N_Sd  è la forza assiale sollecitante di progetto;
• N_Rd  è la forza assiale resistente di progetto;
• f_d  è la resistenza di calcolo a compressione della muratura;
• A  è l’area della sezione trasversale del pannello murario.

Il coefficiente 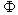_t si ottiene dalla tabella 1 (tabella 4.5.III del D.M. 14/01/2008) in funzione della snellezza (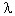) della parete e del coefficiente di eccentricità dei carichi (m).

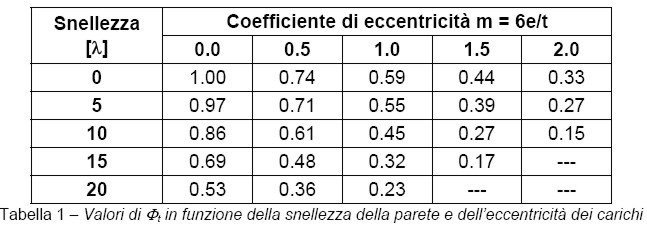
Per valori non contemplati in tabella si procede con l’interpolazione lineare, mentre per valori fuori dai limiti della stessa tabella l’esito della verifica è automaticamente negativo.

Il coefficiente di eccentricità “m” è definito dalla seguente relazione:

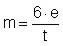                                                                                                    (2)

dove

• t      è lo spessore della parete;
• e    è l’eccentricità dei carichi verticali.

L’eccentricità totale sulla testa del muro si ottiene dalla seguente:

                                                                                           (3)

dove e_s è l’eccentricità dovuta a tutti i carichi che gravano sulla parete, mentre e_a è l’eccentricità dovuta ai difetti di realizzazione della parete e data dalla seguente:

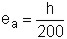                                                                                                (4)

La snellezza della parete si ottiene dalla seguente relazione:

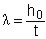                                                                                                    (5)

dove

• h₀        è la lunghezza libera di inflessione del muro pari a 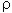∙ h;
• h          è l’altezza della parete;
• t           è lo spessore della parete;
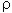•           è il fattore laterale di vincolo dato dalla tabella 2;
• a          è l’interasse tra due pareti ortogonali che irrigidiscono la parete esaminata.

3 – Esempio

All’edificio riportato negli elaborati successivi si deve realizzare la copertura, la quale poggia sui muri perimetrali e su una capriata collocata in una posizione centrale della costruzione (vedi figura 2). L’edificio è realizzato con pareti in muratura il cui materiale è classificabile secondo la Circolare 617/2009 come pietrame disordinata, con spessore di 50 cm ed un’altezza in corrispondenza della linea di gronda pari a 350 cm. Si ipotizza un livello di conoscenza LC1 ed un coefficiente di sicurezza della muratura (_m) pari a 3.

Si riporta negli elaborati successivi la geometria della costruzione.

Figura 2 – Vista in pianta della costruzione

Figura 3 – Vista frontale della capriata

3.1 – Azione assiale sulla testa della parete

Sulla copertura sono previsti i seguenti carichi:

• Peso proprio (comprensivo di capriate):150     daN/m²
• Carico permanente:                                80       daN/m²
• Carico di esercizio:                                 60       daN/m²
• Carico da neve:                                      120     daN/m²

Sulla capriata grava metà del carico dell’intera copertura per una superficie pari a 4.25 × 8.93 = 37.95 m². In definitiva, gravano i seguenti carichi caratteristici:

• Q_pp = 5692 daN        (peso proprio)
• Q_cp = 3036 daN        (carico permanente)
• Q_e = 2277 daN         (carico di esercizio)
• Q_n = 4554 daN         (carico da neve)

Tenendo conto delle combinazioni di carico riportate nel punto 2.5.3 del D.M. 14/01/2008 (combinazione fondamentale), il carico totale che grava sulla capriata è il seguente:

Q_d = 1.3 ∙ 5692 + 1.5 ∙ 3036 + 1.5 ∙ 2277 + 1.5 ∙ 0.5 ∙ 4554 = 18785 daN  (6)

Su ognuno dei due appoggi grava un carico pari alla metà del valore ricavato dalla (6), per cui su ogni parete su cui poggia la capriata si ha uno sforzo normale pari a:

       N_Sd = 9392 daN                                                                                          (7)

3.2 – Resistenza della muratura

Per poter valutare il secondo membro della (1) occorre determinare la resistenza a compressione della muratura. Tenendo presente la qualità della muratura (vedi tabella riportata nel punto C8.A.2 della Circolare 617/2009), del livello di conoscenza LC1 (FC = 1.35) e del coefficiente di sicurezza della muratura (_m = 3) si ottiene:

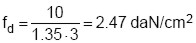                                                                            (8)

3.3 – Verifica con capriata semplicemente appoggiata

Si analizza la parete considerando la capriata semplicemente appoggiata sulla muratura (non si considerano particolari dispositivi di appoggio tra capriata e muratura).

3.3.1 – Sforzo normale resistente (N_Rd)

Per valutare il secondo membro della (1) occorre determinare il coefficiente 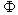_t, funzione del coefficiente di eccentricità (m) e della snellezza della parete (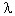). Per valutare l’eccentricità data dalla (3), occorre determinare il punto di applicazione della capriata. A tal proposito, si ipotizza uno sviluppo delle pressioni con andamento triangolare (vedi figura 4) per una lunghezza (l) pari a 1.5 volte l’altezza del solaio (nel nostro caso 1.5 volte l’altezza della catena della capriata).

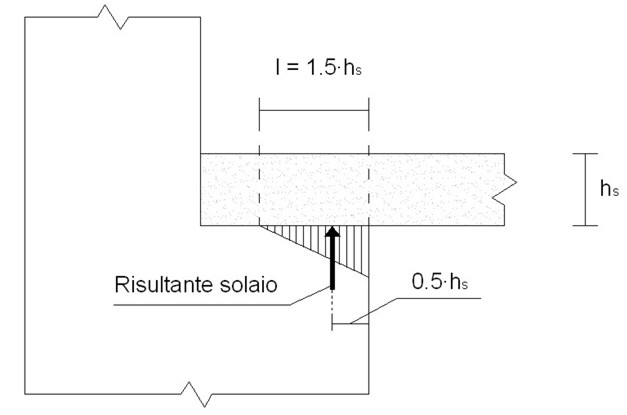
Figura 4 – Risultante dei carichi della capriata sul muro

Visto l’andamento triangolare delle pressioni, la retta d’azione della risultante sarà distante dal lembo interno della parete 0.5 ∙ h_s, pari a 12 cm (altezza della catena pari a 24 cm). Tenendo conto che la parete ha spessore pari a 50 cm, l’eccentricità rispetto al piano medio della parete dovuta alla risultante della capriata è:

e_s = 13 cm                                                                                               (9)

Oltre all’eccentricità riportata sopra, c’è da considerare l’eccentricità dovuta ai difetti di realizzazione (e_a) che nel nostro caso vale:

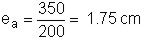                                                                              (10)

In definitiva, l’eccentricità totale è:

e = 13 + 1.75 = 14.75 cm                                                                        (11)

Dalla (2) si ottiene il coefficiente di eccentricità (m):

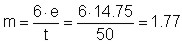                                                                          (12)

La snellezza si ricava dalla (5). Per determinare il coefficiente 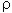occorre valutare l’interasse tra le pareti ortogonali che tendono a contrastare la parete di verifica. Nel nostro caso, poiché la parete di verifica è quella su cui poggia la capriata, possiamo considerarla non contrastata in quanto delimitata da aperture (vedi figura 2). Di conseguenza, il coefficiente 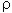si considera con il valore massimo ammissibile, pari ad 1. In definitiva si ottiene:

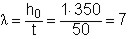                                                                                  (13)

Noti m e 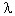, dalla tabella 1 si può ricavare il coefficiente 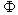_t (valore compreso tra 0.15 e 0.39). Il valore esatto può essere calcolato attraverso interpolazione ed è riportato sotto:

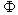_t = 0.2772                                                                                          (14)

Note tutte le quantità necessarie, attraverso la (1) è possibile determinare l’azione assiale resistente:

N_Rd = 0.2772 ∙ 2.47 ∙ 210 ∙ 50 = 7189 daN                                           (15)

3.3.2 – Esito della verifica

L’azione assiale sollecitante (N_Sd) è maggiore di quella resistente (N_Rd), per cui l’esito della verifica è negativo. Il coefficiente di sicurezza è:

s = N_Rd / N_Sd = 0.765                                                                            (16)

Questo comporta che la presenza della copertura destabilizza la parete per effetto delle eccentricità eccessive, restituendo verifiche negative.

3.4 – Verifica con capriata collegata attraverso dispositivo metallico

L’appoggio viene realizzato come riportato in figura 5. La capriata viene appoggiata su due elementi (uno per lato rispetto alla piastra verticale alloggiata nella catena) di dimensioni 10×10 cm di apposito materiale (per esempio neoprene). I due elementi della capriata vengono collegati attraverso due piastre esterne tenute insieme da bulloni. Sulla muratura si realizzano due cordoli metallici con profilo L220×80 tenuti insieme da connettori trasversali 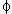20/80 cm. In corrispondenza del punto di appoggio della capriata si realizza una piastra metallica orizzontale saldata sulle ali dei due profili che definiscono il cordolo (vedi anche particolare riportato in figura 7). Sulla piastra orizzontale viene saldata una piastra metallica verticale con appositi fori. Quest’ultima piastra si alloggia all’interno di una cavità realizzata nella catena (in una posizione centrale – la cavità si realizza con uno spessore maggiorato di qualche millimetro rispetto a quello della piastra per ridurre gli attriti tra le parti ed evitare di trasmettere sollecitazioni flessionali).

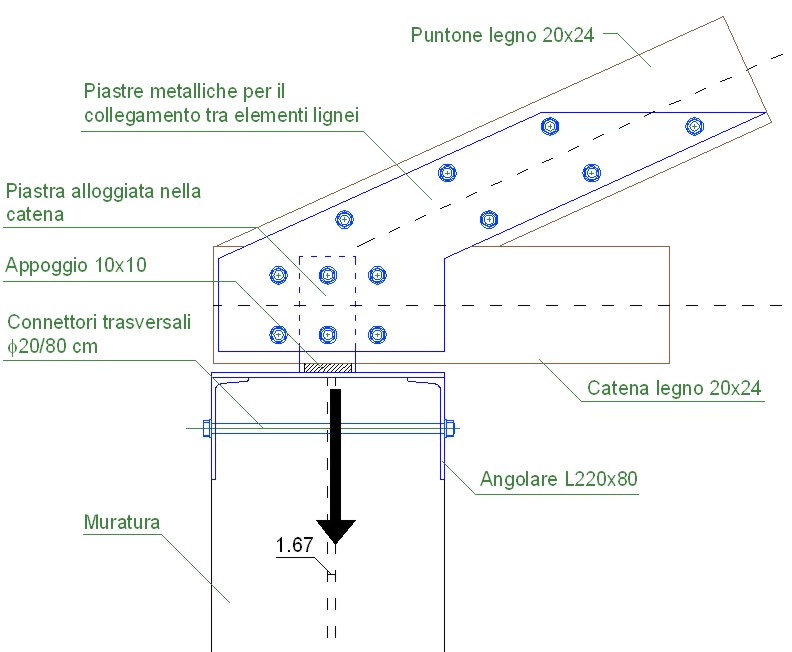
Figura 5 – Collegamento con bassi valori dell’eccentricità

Le piastre che collegano gli elementi lignei (catena e puntone) non vengono realizzati in maniera solidale alla piastra metallica orizzontale in quanto questo può indurre ad uno stato di flessione sulla parete sottostante. In effetti, se la piastra verticale viene saldata a quella orizzontale, anche il semplice attrito tra le parti (se la coppia di serraggio è eccessiva) può trasmettere momento alla parete (vedi figura 6), che non resistendo a trazione si trasforma in una forza concentrata eccentrica.

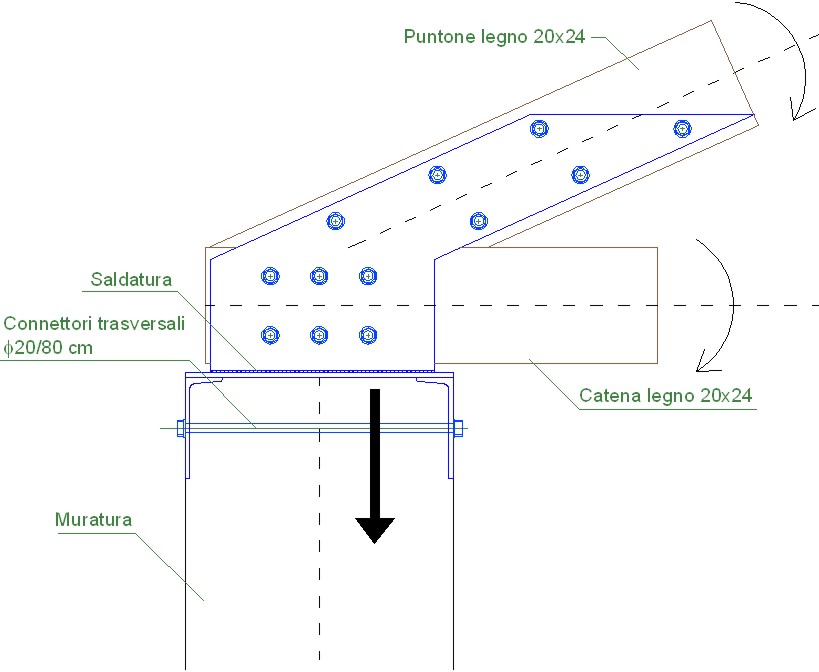
Figura 6 – Collegamento con alti valori dell’eccentricità

Con il collegamento riportato in figura 5, anche se catena e puntone sono uniti in modo rigido tra di loro, il sistema capriata è libero di ruotare rispetto alla muratura, senza creare ulteriori aggravi alla stessa muratura e la retta di azione del carico verticale è molto vicino al piano medio del muro. Un ulteriore vantaggio è che la capriata viene collegata ai cordoli, il che rende un comportamento d’insieme della struttura (si evitano rotazioni relative tra le parti). Le azioni orizzontali dovute alle inerzie della capriata (e della copertura che ci grava sopra) vengono trasmesse ai cordoli che a loro volta le trasmettono alle pareti ortogonali.

3.4.1 – Sforzo normale resistente (N_Rd)

Con il collegamento sopra descritto, la retta di azione trasmessa dalla capriata si trova a 1.67 cm dal piano medio della parete (calcolato con lo stesso criterio visto in figura 4 e riferito solo all’appoggio di larghezza pari a 10 cm). Quest’affermazione comporta una riduzione drastica delle eccentricità, per cui si ha:

e = 1.67 + 1.75 = 3.42 cm                                                                 (17)

Dalla (2) si ottiene il coefficiente di eccentricità (m):

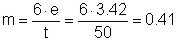                                                                  (18)

Come nel caso precedente (in assenza di dispositivo metallico) la snellezza della parete è data dalla (13). Noti m e 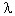, dalla tabella 1 si può ricavare il coefficiente 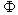_t (valore compreso tra 0.61 e 0.97, molto più alto rispetto al caso con capriata direttamente appoggiata sulla muratura). Il valore esatto può essere calcolato attraverso interpolazione ed è riportato sotto:

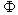_t = 0.878                                                                                         (19)

Note tutte le quantità necessarie, è possibile determinare l’azione assiale resistente:

N_Rd = 0.878 ∙ 2.47 ∙ 210 ∙ 50 = 22771 daN                                        (20)

3.4.2 – Esito della verifica

L’azione assiale sollecitante (N_Sd) è minore di quella resistente (N_Rd), per cui l’esito della verifica è positivo. Tenendo conto della (7) e della (20), il coefficiente di sicurezza è:

s = N_Rd / N_Sd = 2.42                                                                            (21)

3.5 – Particolari costruttivi del nodo

Si riporta di seguito il particolare costruttivo del nodo. Per le ridotte dimensioni della pagina, molte parti possono risultare poco leggibili, per cui, per una visione più chiara si consiglia di scaricare l’elaborato in formato dwg.

Figura 7 – Particolare costruttivo

4 – Conclusioni

Nel documento è stato messo in evidenza l’importanza della trasmissione dei carichi degli orizzontamenti (o altre forme di carichi) alla muratura. Tenendo conto che la muratura è un materiale non reagente a trazione, risulta essere influenzata negativamente da carichi trasmessi in maniera eccentrica. Prestare attenzione alla progettazione degli appoggi diventa indispensabile soprattutto per le murature con limitate risorse di resistenza, le quali non sarebbero in grado di sopportare ulteriori aggravi dovuti all’eccentricità del carico verticale. Le eccentricità dei carichi abbattono la resistenza di una parete e quindi un appoggio realizzato con eccentricità può comportare un punto di debolezza della struttura. Nei casi in cui si realizzano appoggi con carico eccentrico è opportuno che sia ampiamente verificata la muratura sottostante. Non tenere conto dei suddetti effetti può sovrastimare notevolmente la resistenza della parete e di conseguenza della costruzione. C’è da sottolineare che anche sotto l’azione sismica la parete risente gli effetti dei carichi eccentrici in quanto la parzializzazione della parete riduce la sezione resistente della stessa.