Articolo disponibile anche in formato PDF

La conoscenza del limite deformativo di un tirante assume un ruolo fondamentale nel calcolo dei meccanismi locali (analisi cinematica non lineare).

La rottura di un tirante avviene quando cede una delle sue parti, in particolare quando viene superata la resistenza limite di uno dei seguenti componenti:

1)     Cavo del tirante (T_t);

2)     Muratura su cui grava il tirante (T_m);

3)     Chiave del tirante (T_c).

In definitiva si ha

     T = min(T_t, T_m, T_c)                                                                                       (1)

Per semplicità, ipotizziamo di dimensionare la chiave del tirante in maniera tale che sia molto più resistente del cavo e della muratura (T_c >> T_t, T_m), la precedente può essere scritta come segue:

     T = min(T_t, T_m)                                                                                             (2)

In quest’ultimo caso si hanno le due seguenti possibilità:

1)     Rottura del cavo;

2)     Rottura della muratura.

Se la resistenza della muratura è maggiore di quella del cavo (T_m > T_t), la rottura del sistema tirante avviene per la rottura del cavo. In queste condizioni, raggiunto il limite elastico, il tirante esaurisce la sua deformazione elastica ed inizia a snervarsi (vedi “a” di figura 1). Raggiunta la deformazione ultima, il tirante collassa. Indicando con “l” la lunghezza del tirante, ed attribuendo all’acciaio una deformazione di snervamento pari al 10‰ (come per il comune acciaio da c.a.), consegue che il valore limite dello snervamento (l_p) è pari a:

      l_p = 0.01∙l                                                                                                 (3)

Se la resistenza della muratura è minore di quella del cavo, la rottura del sistema tirante avviene per la rottura della muratura (T_m < T_t). In queste condizioni, raggiunto il limite di resistenza della muratura, si verifica il distacco del cuneo (vedi “b” di figura 1). Poiché la rottura del sistema avviene per la rottura della muratura, l’acciaio del tirante è sicuramente in fase elastica (quando la muratura collassa il cavo del tirante ha ancora risorse elastiche). In formule si ha:

        = E∙;                                                                                                     (4)

        = l / l                                                                                                    (5)

Combinando la (4) e la (5) si ottiene:

       l =  ∙ l / E                                                                                               (6)

Poiché la rottura della muratura si verifica quando si raggiunge il limite ultimo di resistenza della stessa (T_m), la tensione raggiunta nel cavo è:

        = T_m / A                                                                                                  (7)

dove “A” è l’area della sezione trasversale del tirante. Combinando la (7) con la (6) si ottiene:

      l = T_m ∙ l / ( E ∙ A)                                                                                     (8)

Le relazioni (3) e (8) definiscono la deformazione ultima del tirante rispettivamente nei casi in cui la crisi si verifica per la rottura del cavo e della muratura.

Figura 1

Esempio

Calcolare la deformazione limite del tirante riportato in figura 2.

Figura 2

Dati

Spessore della parete (t)	50	cm
Livello di conoscenza	LC1
Diametro del tirante (d)	20	mm
Tipologia chiave	Circolare
Diametro della chiave (D)	30	cm
Resistenza di calcolo dell’acciaio (fyd)	2350	daN/cm2
Resistenza media a trazione della muratura (fctm)	1.2	daN/cm2
Coefficiente di sicurezza della muratura (m)	2.5	daN/cm2
Resistenza media a taglio in assenza di carichi verticali della muratura (fvm0)	0.6	daN/cm2
Tensione media dovuta ai carichi (0)	0.8	daN/cm2
Lunghezza del tirante (l)	500	cm
Coefficiente di attrito (n)	0.4

Soluzione

Il primo passo è quello di calcolare la resistenza del cavo (T_c) e la resistenza della muratura (T_m). Visto la sezione circolare del cavo, la resistenza si ottiene dalla seguente:

                                                                           (9)

La resistenza della muratura si ottiene dal minimo della resistenza a trazione (T_m,a) ed a taglio (T_m,t) della stessa muratura:

         T_m = min(T_m,a, T_m,t)                                                                                 (10)

dove per tiranti con chiave circolare si ha:

                                                                                       (11)

                                                                          (12)

Per calcolare la resistenza della muratura occorre definire i parametri meccanici f_ctd (resistenza a trazione) ed f_vd0 (resistenza a taglio). Tenendo conto del coefficiente di sicurezza della muratura (_m) e del livello di conoscenza adottato (per LC1 si ha FC = 1.35) si ottiene:

                                                                 (13)

                                                                 (14)

Sostituendo nelle (11) e (12) i dati numerici, si ottiene:

Dalla (10) si ottiene:

        T_m = 4524 daN

Per la (2), la rottura del tirante avviene per la rottura della muratura. Sotto queste condizioni, quando il sistema tirante va in crisi, il cavo è ancora in fase elastica. Dalla relazione (8) si ottiene:

Se si desidera incrementare la capacità di deformazione del tirante, occorre far aumentare la resistenza della muratura (T_m) in modo che sia superiore alla resistenza del cavo. Dall’analisi delle (11) e (12) si deduce che la resistenza della muratura aumenta all’aumentare delle caratteristiche meccaniche della muratura e delle dimensioni della chiave. Ipotizziamo di consolidare la muratura con iniezioni di malta in corrispondenza del punto di applicazione del tirante (consolidamento indicato per murature in pietrame disordinato con alta percentuale di vuoti) e di portare a 35 cm il diametro della chiave. Dalla Tabella C8A.2.2 della Circolare 617/2009, si deduce che le caratteristiche meccaniche della muratura possono essere moltiplicate per un coefficiente moltiplicativo pari a 2. 

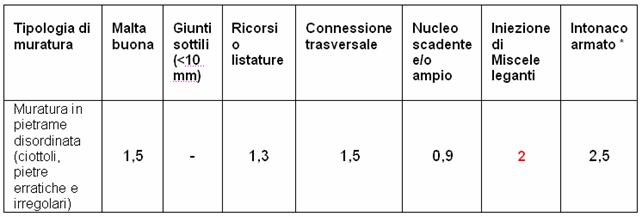
Da queste considerazioni, la resistenza a trazione ed a taglio della muratura diventano:

Dalle (11) e (12) si ottiene:

In questo caso, la resistenza della muratura è maggiore di quella del tirante (quest’ultima pari a 7383 daN), per cui la rottura si verifica per lo snervamento del tirante. Dalla (3) si ottiene:

          l = 0.01∙500 = 5 cm

Come si deduce dall’esempio, la capacità di deformazione del tirante è fortemente legata al tipo di rottura. In alcuni casi, se si ha l’esigenza di incrementare la suddetta deformazione (per esempio, nei casi in cui si effettua l’analisi cinematica non lineare dei meccanismi locali), si può procedere aumentando le dimensioni della chiave (aumenta il diametro D), migliorando le proprietà meccaniche della muratura (aumentano f_ctd ed f_vd0) o riducendo il diametro del cavo del tirante (riducendo opportunamente il diametro del cavo si riduce T_t e di conseguenza la crisi si verifica per la rottura della muratura).

Collana: Calcolo di edifci in muratura

Bibliografia:

Metodi di calcolo e tecniche di consolidamento per edifici in muratura - III edizione - 2019

I tiranti in acciaio nel calcolo delle costruzioni in muratura

I tiranti in acciaio nel calcolo delle costruzioni in muratura

Scarica gratuitamente il software CdT (Calcolo di Tiranti)

Per essere informati